Electronic System of Position Fixing
Hyperbolic Navigation Systems
Hyperbolic Lines
Principle
Loran stations transmit radio signals of very short
duration called pulses. However the frequency of the signals
are quite low about 90 kHz to 110 kHz
Duration of pulse varies and is about 200 μs.
If we assume that a pulse
duration lasts for 200 μs, then:
1 second = 1000000 μs
If the pulse recurring frequency (PRF) is 25pps then-
25 pulses are sent in 1000000 μs
Therefore the interval between each pulse is 1000000/25
= 40000 μs
Or approximately the transmitter transmits a pulse of
200 μs and rests for 40000 μs.
However the power transmitted during these short
bursts is extremely high.
Again we know that radio waves travel at the speed of light, that is at 300000 km per second.
Or in 1000000 μs the
radio waves travel 300000000 metres.
Or in 1 μs the radio
waves travel 300000000/1000000 = 300 metres.
Applying the above we get 1 NM (1852 metres) is
traversed in 6.173 μs
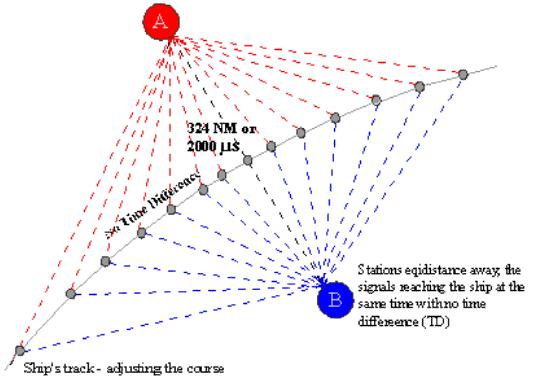
Now let us assume that there are two transmitters (A
and B) separated by a distance of 324 NM.
Radio waves will take about 2000 μs
(324 x 6.173) to traverse from A to B.
Now let both the transmitters transmit at the same
time. Also let a ship be placed at a position where both the signals are
received at the same time. Now let the ship move along a course adjusting her
course so that the two signals are always received at the same time (no time
difference). It is seen that the course line is not a straight line but is a hyperbola.
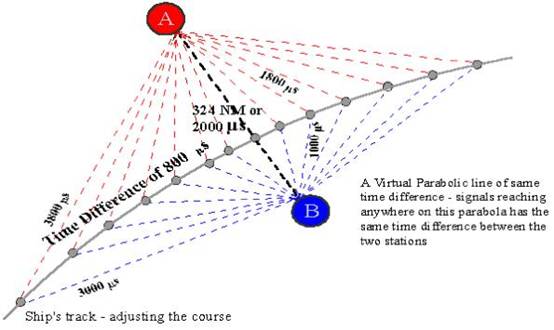
Now it is seen that if there is a time difference in
the arrival of the signals from the two transmitters, then too the track of
equal time difference is a hyperbola. And a ship navigating
with a receiver where the time difference can be recorded need only to keep the
time difference constant to traverse the hyperbola.
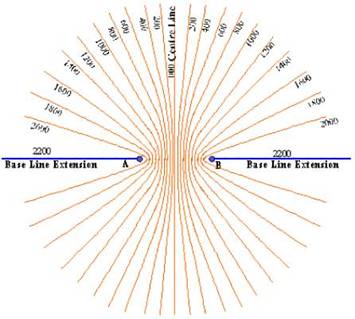
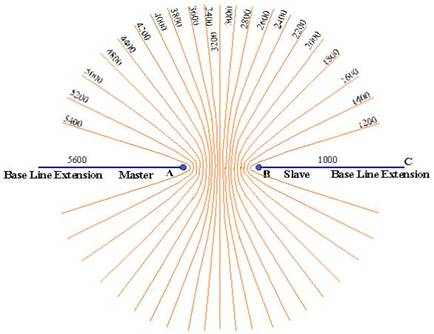
However with multiple hyperbola’s drawn for the same
two transmitters we would have two identical hyperbolas on either side of the
hyperbola of no time difference, as seen in the figure.
The hyperbola of no time difference is known as the
CENTRE LINE. And the line extending between the two transmitters is known as
the base line extension.
Thus in order to resolve the
problem as to on which hyperbola the ship is traversing, we require to create a
time difference between the transmission of the two stations.
So to overcome the above ambiguity, a transmitter
(MASTER) transmits first and after the other station (SLAVE) receives this
signal, it transmits its signal. So the ship will first receive the MASTER signal
and then after a time delay will receive the signal from the SLAVE.
Under this system the time difference between the two
signals will be maximum on the hyperbola near the MASTER station and minimum on
the hyperbola near the SLAVE station.
Since the MASTER signal has to go from the MASTER
station to the SLAVE station and activate it, thus a ship near the MASTER
station will have to wait after getting a signal from the MASTER, for the
signal from MASTER station to go and activate the SLAVE station and then get
the SLAVE station signal.

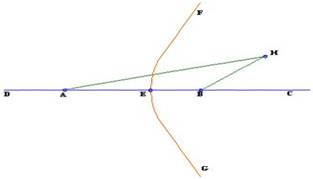
There remains another problem. What happens if at a
point the signal from the MASTER arrives at a time that the signal from the
SLAVE also arrives (after being triggered by the MASTER), and there is no
time difference.
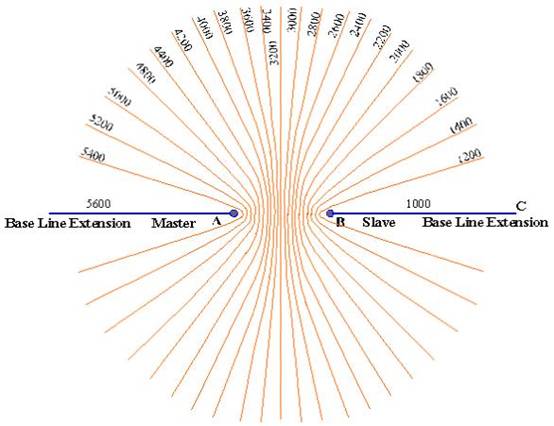
In the above figure, the time difference purposely
created between the transmission of the MASTER station and the SLAVE station is
indicated as 1000 μs on the base line extension.
This time difference is known as the CODING DELAY.
NO coding delay – a ship close to the Slave station Y,
receives signal from M and Y at the same time.
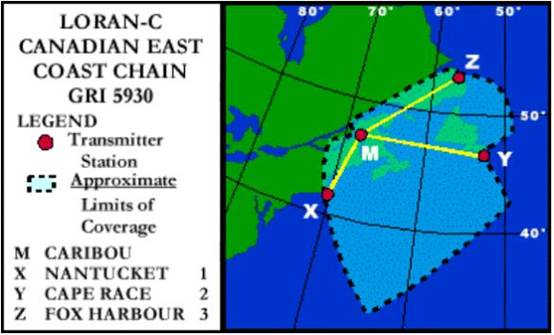
Canadian East Coast GRI 5930
Station Master:
Latitude: 46° 48.’455 North
Longitude: 067° 55.’62 West
Station Yankee:
Latitude: 46° 46.54 North
Longitude: 053° 10.’46 West
A SHIP at location:
Latitude: 46° 44.’54 North
Longitude: 052° 50.’46 West
Distance GC: M to S: 618.97 NM (The signal travels
from M towards S)
M to
Y: 605.139 NM (The signal travels from M towards Y and triggers Y)
Y to
S: 13.85 NM (Signal from Y travels towards S)
618.989
NM