Electronic System of Position Fixing
GPS Systems
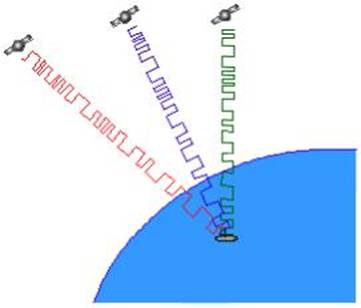
A GPS receiver measures distance from the satellite to
a receiver using the travel time of radio signals.
So we require:
Precise and synchronised
clocks to measure the time difference
The whereabouts of the
satellites
And any signal deterioration or
bending due to atmospheric causes.
Imagine a satellite transmitting
in space.
Then there will occur at
different distances from the satellite a measured time difference in the
arrival time of the signal from the satellite.
Therefore a receiver on the
surface of the earth would by measuring the time difference between the
departure of the signal from the satellite and the arrival at the receiver, be
able to make out the distance from the satellite.
But how is the receiver going to
be informed that the signal has left the satellite. So the receiver has to be
informed of the time. This requires the receiver to have a precision atomic
clock.
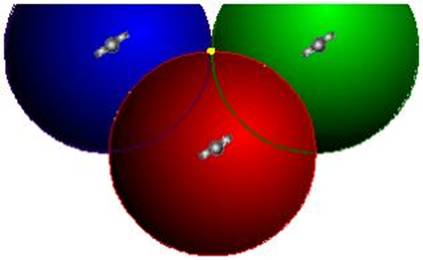
The triangulation is done in the
same manner as are all triangulation’s done. Thus if we assume that the
satellite transmits in all directions including in space, then the signals from
three such satellites will intersect at a point.
But for this to happen the
clocks on the satellites as well as on the receiver have to be atomic clocks,
with absolutely NIL error of synchronisation.
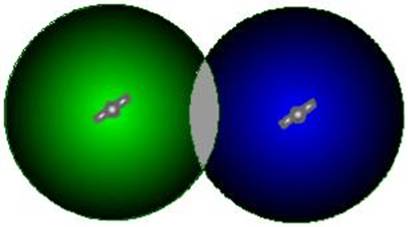
But if the clocks are not
absolutely synchronised as is the case, since
equipping all the receivers with atomic clocks would make GPS beyond the means
of everyone.
The triangulation is done in the above way, taking
into fact that the clocks are not synchronised and
that the triangulation is IMPERFECT.
In
this case then the signals from 2 satellites would intersect as above. And a
receiver anywhere in space would be in the shaded area where the two signals
overlap.
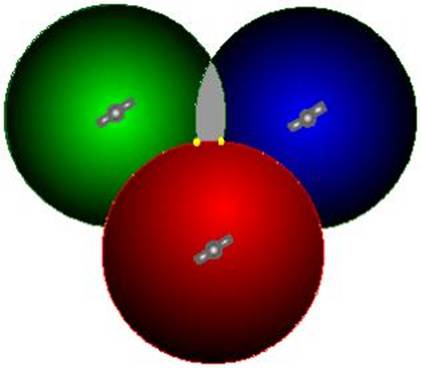
With this IMPERFECT clock system
then, if the third satellite signal is made to overlap then there will exist
only two points in space where the receiver is placed.
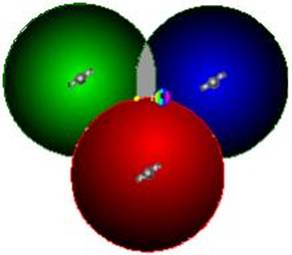
Out of these two positions are
separated by hundreds if not in thousands of miles, additionally one may be in
space while the other will be on the earth’s surface. This
since the signals from all three are received on the surface of the
earth.
Of course a fourth satellite
signal would remove the discrepancy but since the triangulation is solved
practically so the fourth signal is not needed for triangulation.
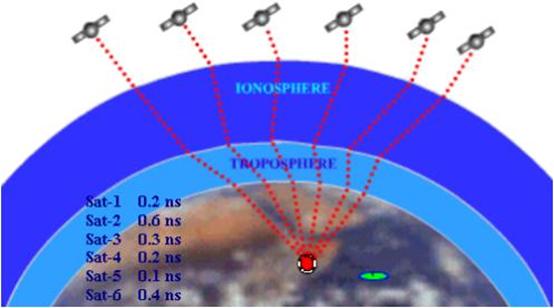
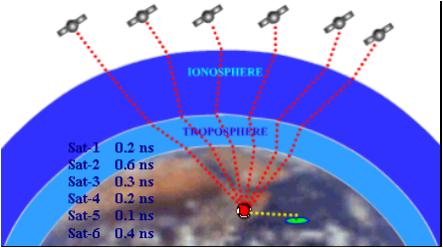
We have now seen that a position
is calculated from distance measurements to at least three satellites.
Now the problem arises of
measuring the distance to a satellite in space
This is done by timing how long
it takes for a signal sent from the satellite to arrive at our receiver.
The Mathematics
In a sense, the whole thing
boils down to a “velocity times travel time” problem.
This simple equation is all that
is used:
Velocity x Time
= Distance
In the case of GPS we’re
measuring a radio signal so the velocity is going to be the speed of light 300,000,000 metres per second.
Synchronisation of Clocks:
The time measurements are
extremely short.
(of
course longer than Radar)
If a satellite were right
overhead the travel time would be something like 0.06 seconds.
The difference in synchronisation of the receiver time minus the satellite
time is equal to the travel time.
Thus we require really precise
clocks.
Even with precise clocks, what
we require is a reference start time.
In a RADAR
we get the reference from the time the signal pulse leaves the magnetron and
the start of the sawtooth current in the CRT. There the time is synchronised. But for satellite signals, the Radio signals
have reached a limit in speed.
So the problem in GPS is how to
have a reference instant.
In the GPS system, if we have a
reference instant then the receiver just has to measure the delay in the signal
reaching the receiver from the satellite and it could then compute the distance
over which the signal travelled.
The GPS satellites transmit
something called a PRC. This PRC is also generated within the receiver at the
same time.
The PRC from the receiver is
matched with that received from the satellite and thus the receiver can easily
compute the time delay, and thus the distance.

Rather than sending just any
radio signal, the satellites send the signal as a code - “Pseudo Random Code”.
Or to be exact a ‘False Random Code’
Each satellite has a unique PRC
Why Random?
The Pseudo Random Code (PRC,
shown above) is a fundamental part of GPS. Physically it’s just a very
complicated digital code, or in other words, a complicated sequence of “on” and
“off” pulses as shown here:
The signal is so complicated
that it almost looks like random electrical noise. Hence the
name “Pseudo-Random.”
PRC
There are several good reasons
for that complexity: First, the complex pattern helps make sure that the
receiver doesn’t accidentally sync up to some other signal. The patterns are so
complex that it’s highly unlikely that a stray signal will have exactly the
same shape.
Since each satellite has its own unique Pseudo-Random
Code this complexity also guarantees that the receiver won’t accidentally pick
up another satellite’s signal.
So all
the satellites can use the same frequency without jamming each other.
And it makes it more difficult
for a hacker to jam the system. In fact the Pseudo Random Code gives the
But there’s another reason for the complexity of the
Pseudo Random Code, a reason that’s crucial to making GPS economical.
The codes make it possible to
use “information theory” to “ amplify “ the GPS
signal. And that’s why GPS receivers don’t need big satellite dishes to receive
the GPS signals.
Each satellite transmits pseudo random noise spread
spectrum signals on two different frequencies,
•L1 at 1575.42 MHz and
•L2 at 1227.6 MHz.
L1 carries the coarse/acquisition code (CA-code) and a
precision code (P-code).
L2 usually only carries P-code, but could carry
CA-code as well.
The CA-code is a short sequence that repeats itself
every millisecond, is different for every satellite, and is known and open to
anyone who wishes to receive and decode it.
The P-code, on the other hand, repeats every 267 days,
and each satellite transmits a different seven-day segment before being reset.
The P-code requires a cryptological
key to decode, which is limited to US Department of Defense (DoD) and other “approved users.”
This pseudo random noise can then be modulated, allowing multiple transmitters to use the same frequency.
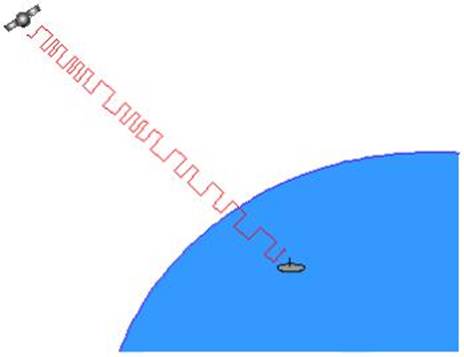
Synchronising the receivers clock and the satellite clock.
If the clocks are not ticking in
unison then there is no way the PRC can be compared for shift.
Since the entire GPS is based on
time difference, the clocks have to be very good, because if the timing is off
by just a thousandth of a second, at the speed of light, that translates into
almost 200 miles of error!
On the satellite side, timing is
almost perfect because they have precise atomic clocks on board.
And
the receivers here on the ground?
Remember that both the satellite
and the receiver need to be able to precisely synchronize their pseudo-random
codes to make the system work.
If the receivers are equipped
with atomic clocks (which cost upwards of $50K to $100K) GPS couldn’t be
affordable.

However the GPS as we know of do
not have atomic clocks, but the receivers still are able to measure time with
an atomic clock precision.
The secret to perfect timing is
to make an extra satellite
measurement.
If three perfect measurements
can locate a point in 3-dimensional space, then four imperfect measurements can do the same thing.
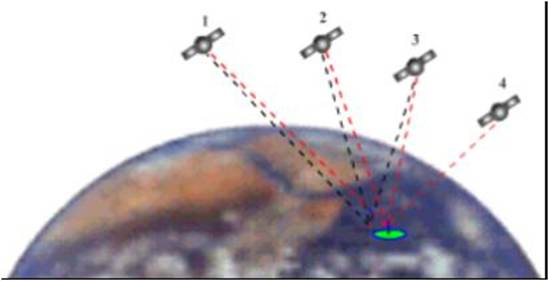
Using
the 4th. Satellite
signal to make a timing correction.
The 4th satellite
gets rid of the imperfect intersection
Extra Measurement Cures Timing
Offset
If the receiver’s clocks were
perfect, then all the satellite ranges would intersect at a single point
-position of the receiver.
But with imperfect clocks, a
fourth measurement, done as a cross-check, will NOT intersect with the first
three.
So the receiver’s computer finds
that a discrepancy in time measurements.
So the receivers
clock is not perfectly synced with universal time.
Since any offset from universal
time will affect all time measurements, the receiver looks for a single
correction factor that it can subtract from all its timing measurements that
would cause them all to intersect at a single point.
That correction brings the
receiver’s clock back into sync with universal time, and - you’ve got atomic
accuracy time right on board.
Once the receiver has that correction it applies to
all the rest of its measurements and gets precise positioning.
Thus all GPS receivers need to
have at least four channels to make the four measurements simultaneously.
So with the PRC as a timing sync
pulse, and this 4th extra measurement, the receiver is perfectly
synced to universal time, and thus can measure the distance to a satellite in
space.
However for the triangulation to
work, the receiver needs also to know where in space the satellite is located.
The receivers start with zero knowledge—they don’t
know where on the planet they are, or what time it is.
Because of this, a good signal from three satellites
is required to determine:
•current time,
•latitude, and longitude, and
•a fourth to also determine
altitude.
Any additional signals increase accuracy.
Most modern GPS receivers are capable of receiving on
12 separate channels.
P-code enabled receivers are able to benefit from
having two different frequencies to lock onto.
This is used to measure the effect the ionosphere is
having on the signals and helps improve accuracy even further.
Since the CA-code is only carried on one frequency,
such measurements are not possible, so an estimate provided by the satellite is
used.
Triangulation based on the CA-code is known as the
Standard Positioning Service (SPS), with the P-code-based system being called
the Precise Positioning Service (PPS).
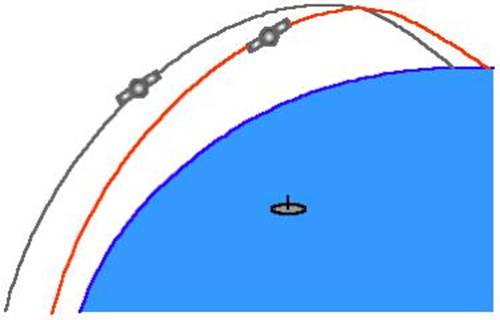
Until now we have assumed that
the position of the satellites is known, so we have used them as reference
points in space.
But do we know exactly where they are? After all
they’re floating around 11,000 miles up in space.
On the ground all GPS receivers
have an almanac programmed into their computers that tells them where in the
sky each satellite is, moment by moment.
The GPS satellites are constantly monitored by the
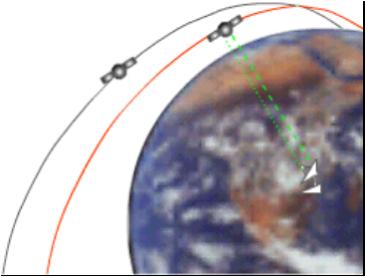
They use very precise radar to
check each satellite’s exact altitude, position and speed.
The errors are called “ephemeris
errors” because they affect the satellite’s orbit or “ephemeris.”
These errors are caused by
gravitational pulls from the moon and sun and by the pressure of solar
radiation on the satellites.
The errors are usually very
slight but they must be taken into account.
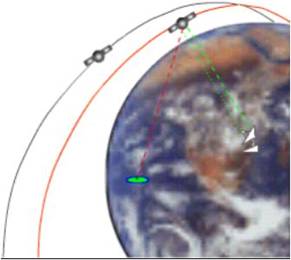
Once the new position of the
satellite is determined it is sent to the satellite which includes its new position as an
information packet with its timing signal.
So the position of the satellite
is continuously updated at the receiver also.
Thus the PRC also contains a navigation
message with ephemeris information as well.
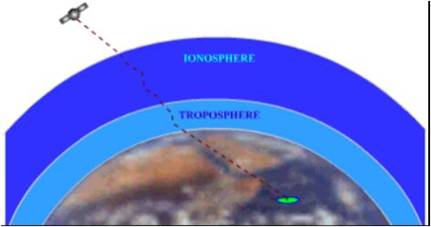
As a GPS signal passes through
the charged particles of the ionosphere and then through the water vapour in
the troposphere it gets slowed down a bit, and this
creates the same kind of error as bad clocks.
There are a couple of ways to minimize this kind of
error. For one thing we can predict what a typical delay might be on a typical
day.
This is called modeling and it
helps but, of course, atmospheric conditions are rarely exactly typical.
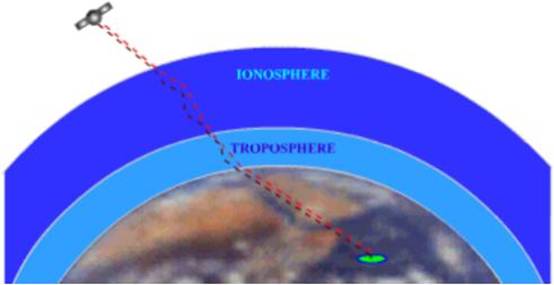 Another
way to get to these atmosphere-induced errors is to compare the relative speeds
of two different signals.
Another
way to get to these atmosphere-induced errors is to compare the relative speeds
of two different signals.

This “ dual
frequency” measurement is very sophisticated and is only possible with advanced
receivers.
The GPS signal may bounce off
various local obstructions before it gets to the receiver.
This is called multipath error and is similar to the ghosting you might
see on a TV.
Problems at the satellite
The satellites also do have to account
for some tiny errors in the system.
The atomic clocks they use are
very, very precise but they’re not perfect. Minute discrepancies can occur, and
these translate into travel time measurement errors.
And even though the satellites
positions are constantly monitored, they can’t be watched every second. So slight position or “ephemeris”
errors can sneak in between monitoring times.

“Geometric
Dilution of Precision” or GDOP.
This depends on the number and
the geometry of the satellites used.
If four satellites are clustered
near each other, then one meter of error in measuring distance may result in
tens or hundreds of meters of error in position.
But if many satellites are
scattered around the sky, then the position error may be less than 1.5 meters
for every meter of error in measuring distances.
The effect of the geometry of
the satellites on the position error is called Geometric Dilution Of Precision (GDOP),
which can roughly be interpreted as the ratio of the position error to the
range error.
Imagine the tetrahedron that is
formed by lines connecting the receiver to each satellite used.
The
larger the volume of this tetrahedron, the smaller (better) the GDOP.
In
most cases, the larger the number of satellites the smaller the GDOP.
Intentional Errors
The policy of “Selective
Availability” or “SA” and the idea behind it was to make sure that no hostile
force or terrorist group can use GPS to make accurate weapons.
Basically the DoD introduced
some “noise” into the satellite’s clock data which, in turn, added noise (or
inaccuracy) into position calculations.
The DoD may have also been sending slightly erroneous
orbital data to the satellites, which they transmitted back to receivers on the
ground as part of a status message.
US military receivers used a decryption key to remove the SA errors and so
they’re much more accurate.
Turning Off Selective
Availability
On May 1, 2000 the White House announced a decision to discontinue the
intentional degradation of the GPS signals to the public beginning at midnight.
Civilian users of GPS are now
able to pinpoint locations up to ten times more accurately.
Sources of Errors for a signal
from the satellite:
Satellite clocks
Ephemeral
Atmospheric
Multipath
Receiver clocks
The GPS receivers use timing signals from at least
four satellites to establish a position.
Each of those timing signals has
some error or delay depending on the climatic conditions experienced before
reaching the receiver.
Since each of the timing signals
that go into a position calculation has some error, that calculation is going
to be a compounding of those errors.
DIFFERENTIAL GLOBAL POSITIONING SYSTEM (DGPS)
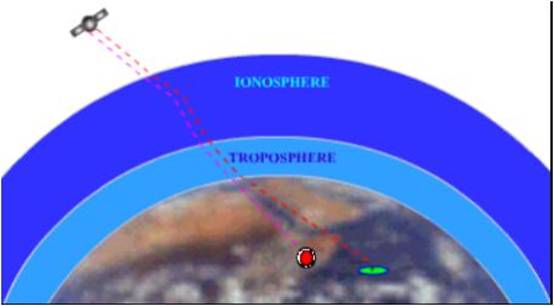
The
satellites are so far out in space that the little distances we travel here on
earth are insignificant.
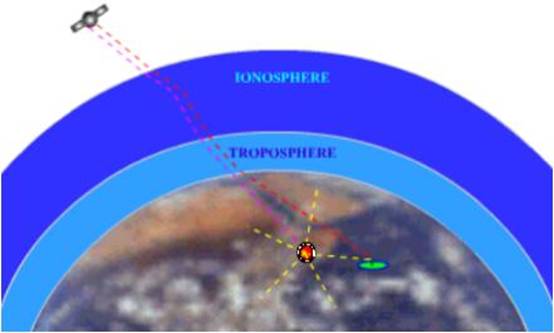
So if two receivers are fairly
close to each other, say within a few hundred kilometers, the signals that
reach both of them will have travelled through
virtually the same slice of atmosphere, and so will have virtually the same
errors
One receiver measures the timing
errors and then provides correction information to the other receivers that are
roving around.
That way virtually all errors
are eliminated from the system, even if the Selective Availability error is
brought in, it would be of no use.
The
idea is simple. Put the reference receiver on a point that’s been very
accurately surveyed and keep it there.
This reference station receives
the same GPS signals as the roving receiver but instead of working like a
normal GPS receiver it attacks the equations backwards. 

Instead of using timing signals to calculate its
position, it uses its known position to calculate timing. It figures out what
the travel time of the GPS signals should
be, and compares it with what they actually are.
The difference is an “error correction” factor. The receiver then transmits
this error information to the roving receiver so it can use it to correct its
measurements.
Since the reference receiver has
no way of knowing which of the many available satellites a roving receiver
might be using to calculate its position, the reference receiver quickly runs
through all the visible satellites and computes each of their errors.
Then it encodes this information
into a standard format and transmits it to the ship receivers.
The ship receivers get the
complete list of errors and apply the corrections for the particular satellites
they’re using.

The
Maritime and Port Authority of Singapore has set up facilities to broadcast
differential GPS signal with effect from 9 Oct.1997.
The aim of providing the DGPS broadcast service is to
further enhance navigational safety.
The service is free of charge
The DGPS service is provided via a marine radio beacon
operating in the MF band at 298kHz at a transmission
speed of 100 bps.
The system provides reliable all weather and round the
clock DGPS data with 99% availability
The DGPS reference station of a channel dual frequency
(L1 & L2) GPS receiver, a MF radio beacon transmitter, an integrity
monitoring station, remote control facilities and back up facilities
The DGPS Reference Station is at a known fixed
position and equipped with sophisticated GPS receivers.
The Reference Station would compare the positions
received from its DGPS receiver with that of the known position and then
generate DGPS data.
The DGPS data is digitally modulated, using Minimum
Shift Keying (MSK), and output via a MF radio beacon transmitter.
The integrity monitoring station would verify the DGPS
signals’ accuracy and ensure that the system provides timely warnings to the
users if and when the system data should not be used.
The DGPS data propagates in the ground wave mode and
the system is designed with a range of 200 km.
The positioning accuracy achievable ranges from ± 5 m
to sub-meter accuracy, depending on the type of receiver used.
The DGPS signal could also be received inland,
offering the same benefits to GPS users on land and in the air.
Technical Details of the
Differential GPS Reference Station
Station ID :
65
Frequency :298 kHz
Bit Rate :100 bps
Modulation :Minimum Shift Keying (MSK)
Data Format :RTCM
Range :200 km
Messages :RTCM Types 9-3, 16, 3, 5 and 7
Facilities :Integrity Monitoring, Remote Control and Back-Up
facilities.
The navigation data message
enables a receiver to calculate the position of each satellite at the time of
transmission of the signal.
From this information, the user
position co-ordinates (Lat/Long) and the user clock bias (error) can be
calculated using simultaneous equations.
Four satellites are normally required to be simultaneously ‘in view of
the receiver for dual-dimensional (3-D) positioning purposes. The following paragraphs give a brief
description of the GPS satellite signals and GPS RCVR operation.
GPS navigation Message
The data includes information required
to determine the following:
Satellite time of transmission
Satellite position
Satellite health
Satellite clock correction
Propagation delay effects
Time transfer to UTC
Constellation status
GPS navigation Message
The navigation message is transmitted
by the satellite on the L1 data link at a rate of of
50 bps.
It is made up of five subframes, subframe 1, 2, 3
contain 10 words, each word have 30 bits.
So
each subframe being 300 bits long.
Subframe 4, 5 are subcommuated 25 time
each.
Every subcommuated
page has 10 words and 300 bits long.
Each 30 bits word contains 24 data bits and 6 parity bits, the parity bits can all be stripped, so every word may
have 24bit (3 bytes) useful.
GPS navigation Message
According to GPS standard
position service (SPS) signal specification, the structure within the
navigation message is as per following table:
Table 4. Navmsg
SUB Total Elapsed
FRAME 0 30 300 bits time
1 TML HOW CLOCK CORRECTION DATA 300 6 sec.
2 TML HOW ephemeris of transmitting satellite I 600 12
sec.
3 TML HOW ephemeris
of transmitting satellite II 900 18 sec.
4 TML HOW page
“n” 0f 25 - messages,
ionosphere, UTC, etc 1200
24 sec.
5 TML HOW page
“n” 0f 25 - almanac,
health status, etc 1500
30 sec.
Note: The subframe
ID number is part of the HOW word.
TML : Telemetry Message
Table
5. Telemetery
message
One word = 30 BITS, 24 DATA, 6 PARITY
word 0 30 300
Total bits
1 TML 8-BIT PREAMBLE 24-BIT DATA 6-BIT
PARITY
HOW : HANDOVER WORD
One word = 30 BITS, 24 DATA, 6
PARITY
Table 6. HANDOVER WORD
word 0 30 300
Total bits
1 HOW 17-BIT TIME OF
WEEK 7-BIT DATA 6-BIT PARITY
The Navigation Message
The NAV-msg
is superimposed on both the P-code and the C/A-code with a data rate of 50
bits/sec.
The NAV-msg
contains 25 data frames, each frame consisting of 1500 bits. Each frame is divided into 5 sub frames of
300 bits each.
It will therefore take 30
seconds to receive one data frame and 12 ‘/2 minutes to receive all 25 data
frames.
Sub frames 1, 2 and 3 repeat the
same 900 bits of data on all 25 frames.
This allows the receiver to
obtain critical NAV-msg data within 30 seconds.
This ensures that the receiver
need not wait for a long period (12 to 15 minutes) to provide the first
position. It can do so within the first
minute.
The data in the NAV-msg is normally valid for a 4 hour period.
The NAV-msg
contains GPS system time of transmission, a Hand Over Word (HOW) for the
transition from C/A to P-code tracking, ephemeris (almanac) and clock data for
the particular satellite being tracked, and almanac data for all the satellite
vehicles (SVs) in the constellation.
Additionally, it contains
information such as satellite health, coefficients for ionospheric
delay model for C/A-code users, and coefficients to calculate Universal
Coordinated Time (UTC).
ACCURACY AND ERROR SOURCES
Accuracy of GPS RECEIVERS
The following factors influence
the final positioning accuracy obtainable with GPS:
The
precision of the measurement and the satellite geometry.
The measurement processing
technique adopted.
The
accuracy with which atmospheric and ionospheric
effects can be modeled.
The
accuracy of the satellite ephemerides.
Accuracy of GPS RECEIVERS
GPS exhibits statistical accuracy
distributions because of two important parameters, which are continuously
variable.
(a) The
(b) The Dilution of Precision (DOP)
UERE is a measure of the error
in the range measurement to each satellite as seen by the Receiver. UERE tends to be different for each satellite
and tends to be at a minimum following an upload.
Accuracy of GPS RECEIVERS
DOP is a measure of the error
contributed by the geometric relationship of the satellites as seen by the
Receiver. DOP varies because the
satellites are in constant motion and their geometric relationships are
constantly changing.
The
above two errors are constantly present as normal variations in Accuracy, even
without failures in the satellites, Control Segment or Receiver.