| Amplitude | Day | Ex Meridian | Exercises | Pole Star | |
| Naut. Almanac |
Celestial Navigation
Ex
First Point of Aries
Nautical Astronomy is an exact science,
if approximation were to be used then the position of a ship would be grossly
in error and may end up with the ship in disastrous situations.
Since the axis of the Earth is tilted to about
23.5˚ the sun is assumed to travel around on the ecliptic. This ecliptic
cuts the celestial equator at a point called the ‘First Point of Aries’. Since
this is as constant as can be obtained the reference point for most of nautical
astronomy is this point.
All the stars are referenced to this point, the Hour
Angle West of the ‘First Point of Aries’ is called the Sidereal Hour Angle
(SHA) and this is tabulated for each star in the Nautical Almanac.
The Greenwich Hour Angle of a star is thus found out
by obtaining the GHA (Aries) from the Almanac and then adding the SHA of that
particular star.
So instead of having the GHA of each star tabulated
for each hour, it is convenient to use a constant like the GHA (Aries), which
is tabulated for every hour, and then adding the SHA to obtain the GHA (star).
Ex
If the sun is not available during the time of her
passage across the meridian – meridian passage then the following observations
and calculations are done to obtain the latitude.
This method is only applicable to bodies close to the
meridian and the HA of the body should not exceed one hour. The thumb rule
being that the HA in minutes should not exceed the number of degrees in the
meridian zenith distance nor should the meridian zenith distance be less than
25° except under most favourable conditions.
To start off the altitude of the body is taken
together with the GMT, this to obtain the HATS which should be accurate.
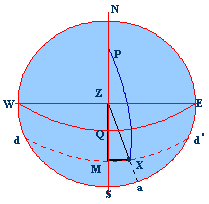
In the above we have the observer at Lat. 43° and the
body (sun) with a declination of 22°. The sun is approaching the meridian – it
is better to take an ex.
WQE is the equinoctial
WZE is the prime vertical
NZS is the observer’s meridian
dMXd’ the
parallel of declination
P the pole, Z the zenith, X the sun at the time of
observation
M the position of the sun when it is on the meridian
Angle ZPX is the East HA of the Sun (X)
PZ the co-latitude
ZQ the latitude
PX the polar distance (90°+
decl.)
ZX the zenith distance of the body (Sun)
ZM the zenith distance when the sun is on the meridian
that is it is the MZD (Meridian Zenith Distance)
ZQ the latitude = (ZM – QM), that is (MZD – decl.)
We have to find ZM the meridian zenith distance.
The least distance of a body occurs when the body is
on the observer’s meridian that is at MP, so the zenith distance at any other
time must be greater than the MZD and therefore in the above example ZX is
greater than ZM.
Thus the calculation of finding the arc ZM is called
‘Reduction to the
The reduction referred above is a very small quantity,
which is the difference between the MZD and the observed zenith distance: arc
ZX – arc ZM
But the body is so close to the meridian that PX is
practically equal to PM and if
(PM – PZ) is equal to ZM, then (PX – PZ) is assumed to
be assumed to be also equal to ZM, the meridian zenith distance which we are
out to find in triangle PZX.
Now a DR latitude has to be
introduced into the above calculation so that the latitude found out may be
approximate to the actual latitude.
If the calculated latitude should differ greatly from
the DR latitude the triangle has to be reworked, using the new latitude so as
to obtain a nearer approximation.
Many Ex _
Using Nories Tables
Let us work with an LHA (sun): 352°44.2’
Declination:
21°49.5’S
Latitude:
42°18.0’ N
Enter Table I with:
Lat. 42°18.0’ N, decl. 21°49.5’S (different names) and
get 1.5” (A)
Now enter Table II
LHA 352°44.2’ and (A) as 1” and get 14.05(*1)
LHA 352°44.2’ and (A) as 0.5” and get 7.03 (*2) (here read the value for 5”
and then shift the decimal point to get for 0.5”)
Therefore adding for a total of 1.5” would give a
result of 21.08, and this is the ‘Reduction’ to be subtracted from the observed
zenith distance.
Obs. Zenith
Dist. 64°32.00
Reduction 21.08
Therefore MZD 64°10.92
N
Declination 21°49.5
S
Latitude at sight time = 42°21.4’ N