Back to Nautical	Solar Sys.	Celestial Sphere	Hour Angles	PZX Triangles	Dip
	Amplitude	Day	Ex Meridian	Exercises	Pole Star
	Naut. Almanac

Celestial Navigation

Exercises

Latitude by Meridian Altitude STAR

Date: 31.10.1998.

Sext Altitude: 57°25’

Star: Acrux

Declination: 63°05.3’S

Bearing: South of observer

IE: 3.3’ OFF the arc

Height of Eye: 6 m

Latitude: ??

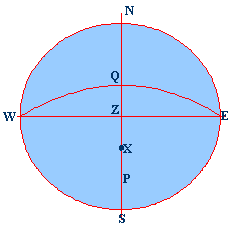
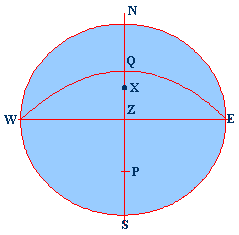
NESW is the rational horizon

P is the pole

Z is the Zenith

X is the Star

WQE is the celestial equator

WZE is the prime vertical

NZS is the observer’s meridian

ZX is the zenith distance

SX is the true altitude

PX is the polar distance

QX is the declination

PZ is the co-Lat.

QZ is the Latitude

Correct the Altitude:

Sext. Alt.: 57°25.00’

IE: + 3.3’ (OFF)

Observed Altitude: 57°28.3’

Dip: (-) 4.3’ [Dip (in minutes) = 1.76√Height of Eye (in metres)]

57°24.0’

Refraction: (-) 0.6’

True Altitude: 57°23.4’

(-) 90°00.0’

True Zenith Distance: 32°36.6’N

Declination: 63°05.3’S [Same names add, different names subtract]

Latitude: 30°28.7’S

Calculating the Meridian Altitude STAR

Date: 01.11.1998.

Sext Altitude: 57°25’

Star: Altair

Declination: 08°52.1’N

Bearing: South of observer

IE: 2.0’ ON the arc

Height of Eye: 7 m

DR Latitude: 44°14.0’N (approximate)

DR Longitude: 158°00.0’E

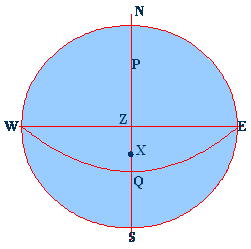
NESW is the rational horizon

P is the pole

Z is the Zenith

X is the Star

WQE is the celestial equator

WZE is the prime vertical

NZS is the observer’s meridian

ZX is the zenith distance

SX is the true altitude

PX is the polar distance

QX is the declination

PZ is the co-Lat.

QZ is the Latitude

Correct the Altitude:

DR Latitude: 44°14.0’N

Declination: 08°52.1’N [Same names subtract, different names add]

{Since this is reverse calculation to find the altitude, the add / subtract rules change}

Approx. MZD 35°21.9’N

(-) 90°00.0’

Approx. True Altitude: 54°38.1’ S

Refraction: (+) 0.7’ Reversed signs since we are doing the calculation backward

Dip: (+) 4.6’ [Dip (in minutes) = 1.76√Height of Eye (in metres)]

IE: + 2.0’ (ON) this is not reversed, since this a equipment fault

Approx. Sext. Alt.: 54°45.4’S

Latitude by Meridian Altitude STAR

Below the Pole

FINDING THE LATITUDE

Date: 06.11.1998

Sext Altitude: 15°08’ North of the observer

Longitude: 158°00.0’E

Star: Alioth

Declination: 55°58.0’N

Bearing: North of observer

IE: 1.6’ OFF the arc

Height of Eye: 10 m

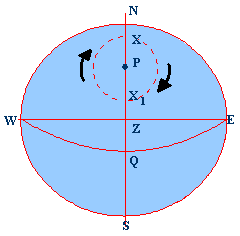
NESW is the rational horizon

P is the pole

Z is the Zenith

X is the Star below the pole

WQE is the celestial equator

WZE is the prime vertical

NZS is the observer’s meridian

ZX is the zenith distance

PX is the polar distance

QX is the declination

PZ is the co-Lat.

NX the True Alt. Below the pole

QX1 is the declination

NP is the Latitude

Declination: 55°58.0’N

(-) 90°00.0’

Polar Distance: 34°02.0’

Sext. Alt.: 57°25.00’ N

IE: + 1.6’ (OFF)

15°09.6’

Dip: (-) 5.6’ [Dip (in minutes) = 1.76√Height of Eye (in metres)]

15°04.0’

Refraction: (-) 3.6’

True Alt.: 15°00.4’ N

Polar Distance:(+) 34°02.0’

Latitude: 49°02.4’N (Explanation See figure)

Important: When the object is on the meridian below the pole it always bears North in North Lat., and South in South Lat. Or you may say that the Latitude always has the same name as the bearing of the object.
Latitude by Meridian Altitude STAR

Below the Pole

FINDING THE ALTITUDE

Date: 31.10.1998.

DR Latitude: 48°04.0’ S

DR Longitude: 120°00.0’E

Star: Achernar - Below the Pole

Declination: 57°14.7’N

Bearing: North of observer

IE: 1.5’ ON the arc

Height of Eye: 8.5 m

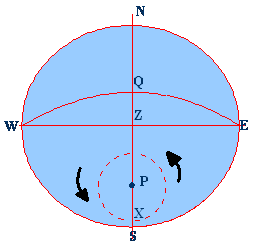
NESW is the rational horizon

P is the pole

Z is the Zenith

X is the Star below the pole

WQE is the celestial equator

WZE is the prime vertical

NZS is the observer’s meridian

ZX is the zenith distance

PX is the polar distance

QX is the declination

PS is the Lat.

PZ is the co-Lat.

NX the True Alt. Below the pole

NP is the Latitude

SX is the Altitude.

Declination: 57°14.7’N

(-) 90°00.0’

Polar Distance: 32°45.3’

DR Latitude: 48°04.0’S

Polar Distance: 32°45.3’ (Explanation See figure)

Approx. True Altitude: 15°18.7’

Refraction: (+) 3.4’Reversed signs since we are doing the calculation backward

Dip: (+) 5.1’ [Dip (in minutes) = 1.76√Height of Eye (in metres)]

IE: + 1.5’ (ON) this is not reversed, since this a equipment fault

Approx. Sext. Alt.: 15°28.7’S

SUN

Latitude by Meridian Altitude

The sun is on the observer’s meridian at noon Local Apparent Time.

The Local Mean Time of the MP at GREENWICH is given in the Almanac – Sun Mer Pass.

The above is the approximate time of MP at any other meridian.

Process:

Take down the time of MP of the Sun: Name it Local Mean Time of MP

Convert the Longitude into Time – Long. (W) (+) and Long. (E) (-)

Add or subtract the Longitude in time from the LMT to get the GMT of the MP

Look up the Almanac to get the Sun’s declination – correct it as required.

Find the TZD from the T.Alt.

Add or subtract the declination to the TZD to get the Latitude.

Date: 06.11.1998.

00h 12h

Equation Of time 06th------------------- 16m23s 16m22s

Equation of time 07th------------------- 16m21s 16m19s

Now interpolate for --------------------- 14h 11m 00s

LAT (ship)--------------------------------- 12 00 00

Long. WEST-------------------- (+) 02 11 00

Greenwich Apparent Time (GAT) 14 11 00

Equation of Time-------------- (+) 16 22

GMT (Noon at ship) 14 27 22

Sext Altitude: 63°50.0’ North of Observer

Bearing: North of observer

IE: 3.3’ OFF the arc

Height of Eye: 7 m

Latitude: ??

Longitude: 032°45.0’W

NESW is the rational horizon

P is the pole

Z is the Zenith

X is the Star

WQE is the celestial equator

WZE is the prime vertical

NZS is the observer’s meridian

ZX is the zenith distance

NX is the true altitude

PX is the polar distance

PZ is the co-Lat

QX is the declination

ZQ is the Latitude.

QZ is the Latitude

Correct the Altitude:

Sext. Alt.: 63°50.0’

IE: + 3.3’ (OFF)

Observed Altitude: 63°53.3’

Dip: (-) 4.8’ [Dip (in minutes) = 1.76√Height of Eye (in metres)]

Convert the Longitude into Time.

Divide the Longitude by 15°

So, 032°45.0 = 02h 11m

GMT = MP + Long. (W)

D H M

LMT 06 11 44

Long W + 02 11

GMT 06 13 55

63°48.5’

Refraction: (-) 0.5’

63°48.0’

Parallax: (+) 0.1’

Semi Diameter: (+) 16.2’

True Altitude: 64°04.3’

(-) 90°00.0’

True Zenith Distance: 25°55.7’ (ZX)

Corrected Declination: S 16°01.3’ (QX)

Latitude: 41°57.0’ (ZQ)

SUN

FINDING THE LONGITUDE

Date: 03.11.1998.

Time: ------------------ 0800

DR Latitude: ---------- 32˚06.0’N

DR Longitude: -------- 140˚54.0’E

Chron. Time: --------- 03d 22h 02m 07s

Chron. Error: SLOW----------- 00m 40s

Sext Altitude: --------- 36°01.0’ (sun LL)

IE: --------------------- 3.6’ ON the arc

Height of Eye: -------- 12.2 m

Chron. Time:--------------- 03 22 02 07

SLOW----------------------- (+) 00 40

GMT------------------------- 03 22 02 47

GHA (sun) For 22h------- 154˚06.3’

Incr.For 02m 47s---------- (+) 0˚41.8’

GHA ------------------------- 154˚48.1’

Decl-------------------------- 15˚12.7’S

-------------------------------- (-) 90˚00.0’

Polar Distance ------------ 74˚47.3’ (PX)

PZ – PX--------------------- 16˚53.3’

PZ – ZX--------------------- 03˚59.9’

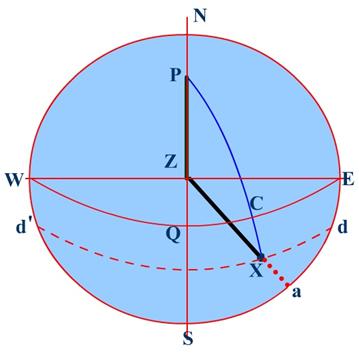
NESW is the rational horizon

P is the pole

Z is the Zenith

X is the Sun

WQE is the equinoctial

WZE is the prime vertical

NZS is the observer’s meridian

ZX is the zenith distance

NX is the true altitude

PX is the polar distance

CX is the Declination

aX is the altitude

PZ is the co-Lat

Angle ZPX is the Hour Angle

Angle PZX is the Azimuth

Known: PZ, PX, AND ZX.

To find: angle P and angle Z

Correct the Altitude:

[Dip (in mts) = 1.76√Height of Eye (in m)

Sext. Alt.(LL):------------ 36°01.0’

IE:-------------------------- (-) 3.6’ (ON)

----------------------------- 35°57.4’

Dip:------------------------- (-) 6.2’

----------------------------- 35°51.2’

Corr. (Almanac)---------- (+) 14.7’

True Altitude:------------- 36˚05.9’

------------------------ (-) 90°00.0’

True Zenith Distance:---- 53°54.1’ (ZX)

Latitude:----------------- 32˚06.0’N

------------------------ (-) 90°00.0’

Co-Lat. 57°54.0’ (PZ)

	Longitude = LHA ~ GHA LHA (sun):-------- 301˚48.7’ GHA (sun):-------- 154˚48.1’ ----------------------- 141˚02.7’ E Obs. Longitude:----------- 147˚00.6’ E

Once the Longitude has been found out, the position line that has been obtained is plotted on the position of DR Latitude and the Observed Longitude.

From the above calculation it is apparent that the DR Latitude plays an important part in determining the observed Longitude, thus if the position of the DR Latitude is in error then the obs, Longitude will be way out.

However the Azimuth will not be since a slight error in Latitude will not make much difference in the Azimuth.

WORKING ON BOARD:

In ancient times – before the advent of GPS, the sight of the sun was of paramount importance, since this was one of the primary means of locating the position of a ship. Observation of stars was not that fortunate because the horizon had to be good and the cloud cover negligible.

The Sun as a result was observed in the Morning at around 0800h and the Longitude obtained. At Noon, the MP of the sun was observed and the position line obtained from the morning sight was transferred to the Noon position, thus the Observed Latitude and the transferred Position line gave the observed position of the ship. In the late afternoon, the sun was again observed to check up on the accuracy of the position as well as for any extraordinary drift, the speed and drift being taken as estimated.

In this we would be using the figures as obtained in the above example.

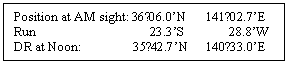
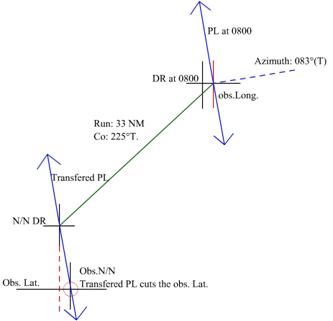
After the Sun was observed in the morning the Ship sailed a distance of 33 NM on a course of 225˚T.

Principle of Position Lines

Celestial Sphere Showing the Earth and the 2 stars. The projected spots of the stars on the surface of the Earth

In the above we see two heavenly bodies as viewed from the earth, they are projected on the imaginary celestial sphere. The positions of the two bodies if projected on the earth would be at their respective GP’s as shown in the other figure (marked as X)

We may assume any latitude or longitude of the GP’s of the two bodies.

Now with the True Zenith Distance as observed, we may draw a circle with radius equal to that of the TZD on the surface of the Earth.

Then at every point on the circle the observed altitude (true) would be the same since it is a circle of equal TZD of that body.

However distant a ship may be as long as the location of the ship is on the circumference of the circle the TZD as found would be the same.

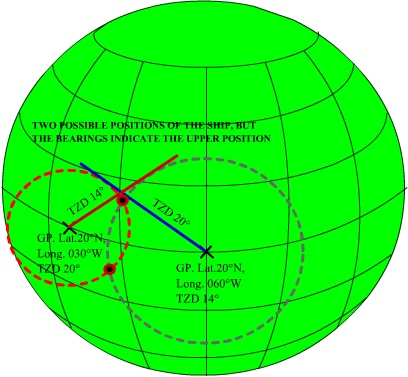
Let us now assume the following that the body has a declination of 20°N and a GHA of 2 hours, then this body’s GP would be at lat. 20°N and Long. 030° W.

Let the body as observed have a true altitude of 70°, then the TZD would be 20°

A ship from which the bearing of the body is due North would be on the equator and on the same meridian as the body. That is the ship would have a position of Lat. 00° and Long. 030°W. This because the line of bearing, North cuts the circle at a definite position.

However from another ship if the same body is observed as bearing 180° then that ship would be on a parallel of latitude that is 20° due north of the GP of the body, or the Latitude of the ship would be 40°N. The longitude would be same at 030°W. This because the line of bearing, South, cuts the circle at a definite position.

Again if another ship observes the body on a bearing of 116° True then, this line of bearing would cut the circle at the ships position as shown in the figure.

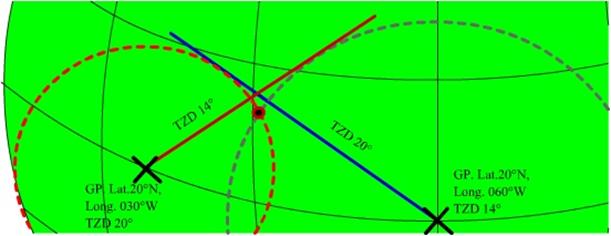
If this above ship takes another observation now of a different body whose declination is the same at 20°N but the GHA is at 4 hours, its GP would be would be lat. 20°N and Long. 060°W. Let the TZD as obtained from the observed altitude to be 14° and the bearing from the ship as 225°. Then the ship’s position as referenced to this body would lie on the dotted line where the dotted line cuts the circle.

Thus if a ship observes two or more bodies at the same time (nearly) the points of intersection of the bearing lines would give the position of the ship with some degree of accuracy. However the points intersect at two opposite directions, thus the bearings of the bodies from the ship would determine the exact position of the ship.

So far so good.

But we cannot draw such huge circles and accuracy would suffer. So instead of drawing the circles what we do instead is we draw a part of the arc, this arc although a curved line may be assumed to be a straight line for a very short length.

The question is now of fixing the centre of the body, this is overcome by estimating the position of the ship – that is using the DR position of the ship.

Now since the body/ bodies are observed from this DR position the line of bearing would pass through this position.

The Zenith Distance of the body is calculated for the time of observation, and the Zenith Distance as obtained from the observation of the altitude is compared.

Or the CZD is compared with the TZD.

If the TZD and the CZD are the same then the Ship is at the position of the DR. The arc of the circle (which is drawn as explained earlier with the radius as the TZD) would be drawn at right angles to the line of bearing (since the radius always cuts the circumference at right angles – the arc of the circumference being a straight line as assumed). If two or more bodies have been observed and assuming that the ship was stationary during the observation (there being absolutely no movement of the ship) and also that the observer was a genius at sights then theoretically the arcs (straight lines representing the arcs) would all intersect at exactly the DR and the DR would be the observed position of the ship.

However if the arcs do not intersect then the point at which they do intersect becomes the observed position of the ship.

But when comparing the CZD and the TZD, the difference, called the ‘Intercept’ may be +ve or –ve.

Or we may say that CZD is more than TZD by a value or the reverse. In that case how do we draw the line of bearing and where do we place the arc of the circle of position?

First we mark the DR of the ship and the bearing lines are drawn since the DR position is close to the actual position and the bearing was taken from that location the bearing line would pass through the DR position.

Now the question where do we draw the arc (straight line) on the bearing line, obviously it will be at right angles to the bearing line as a radius always touches the circle at right angles.

Modifying the figure for ease in drawing on the chart paper, we have:

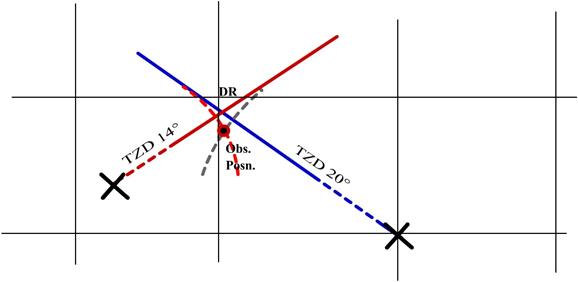
Here we see that the Body positions are very far in the distant – the dotted lines indicate this.

Also the arcs are shown as arcs, but when we draw on the ship we would use straight lines. Also the arcs are drawn centered on the bodies. Whereas the arcs or the straight line we would be drawing would be centered on the DR position.

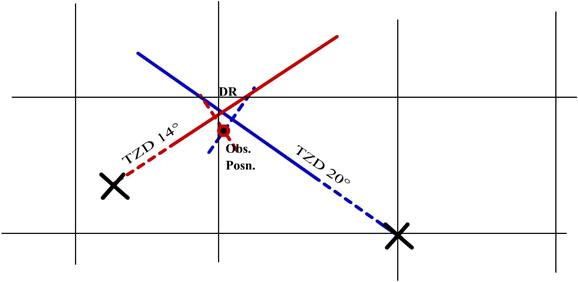
What has been shown above is the observed position as plotted with the TZD, but this again is not possible on the ship, since we still cannot plot the GP of the bodies.

Thus on the ship we first calculate the Zenith Distance for the time of observation using the details given in the Almanac.

Next we find the true altitude and obtain the True Zenith Distance.

Next we compare the CZD with the TZD. If we have the CZD is greater than the TZD then:

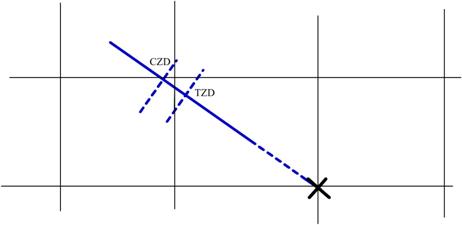
The ship is somewhere on the approx. arc of CZD, the actual position is however on the ARC of the TZD circle.

In the above since the CZD (estimated) radius is more than the actual radius that is the TZD, therefore the ship has to be on the arc TZD, so we term this difference between the CZD and the TZD as TOWARDS, that is we are moving towards the body for accuracy.

If however the TZD had been greater then the Ships position would have to be shifted on to the TZD arc which being greater, meant that the ship was being moved AWAY from the body.

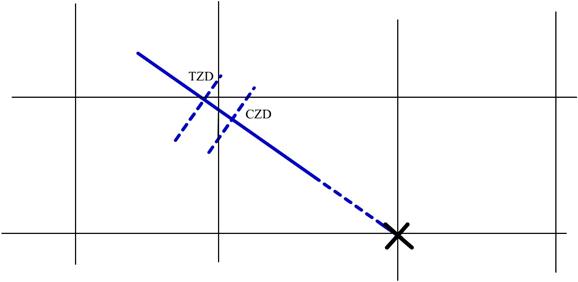
Summing up:

For plotting we first calculate the CZD using the time of sight and the Almanac, the ship is on the arc drawn with the CZD as radius – this is the assumption.

Next we calculate the TZD using the observed altitude.

We compare the two, and find which one is greater, if:

CZD is greater than TZD then the difference (Intercept) is termed TOWARDS

TZD is greater than CZD then the difference (Intercept) is termed AWAY.

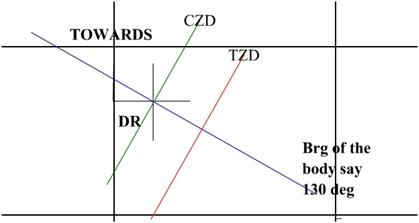
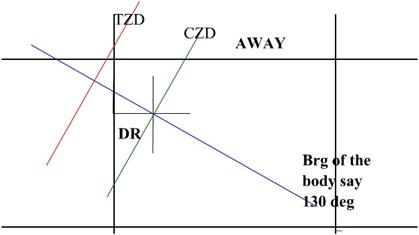
If two or more bodies were observed then the ship would lie at the intersection of the arcs – Position Lines.

After the above position lines have been drawn, the intersection of the position line forms the position at which the ship was at the time of observation.

This plotting may be done on any chart (old and cancelled – preferably of a region close to the equator)

The intersection position is now measured with reference to the DR.

The distance above or below the DR is measured using a fixed scale, which was used for the initial marking of the Intercept. And the distance so measured is considered as the Difference of Latitude to the DR latitude.

The distance east or west of the DR is considered as the departure from the DR Longitude.

Applying the D’lat we find the OBS. LATITUDE.

Using Traverse table and the mean of the two latitudes we can convert the Departure measured into Difference of Longitude and applying this to the DR Longitude we would get the OBS. LONGITUDE.

In general working the scale used is the Longitude scale, since the Longitude scale remains constant on a Mercator chart but not the Latitude scale.

NOTE: The time interval between the sights of the bodies if too long then run between the individual sights have to be applied, however if the entire time period is less than 3 minutes then the run interval may be omitted due to the distance run being insignificant. Practicing the shooting of the stars, makes taking up to 4 stars complete, within 3-4 minutes.

The Marcq St. Hilaire method of fixing the position of the Ship

(Also known as the Intercept method)

In this method the TZD is compared with the CZD and the Intercept is found out. The position of the PL may have to be drawn Towards the body or Away from the body.

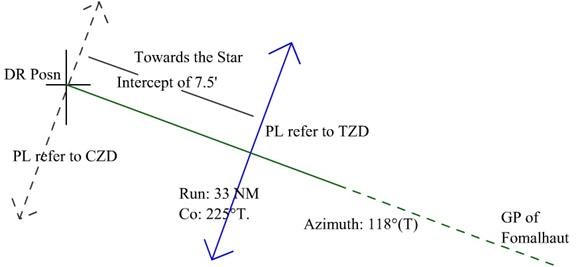
Let us now assume that another two stars were observed at an interval of time of 30s – say practically the same time.

The DR used for calculation remains the same.

We have Fomalhaut with an azimuth of 118˚T giving a PL of 028˚ - 208˚ and with an Intercept of 7.5’ Towards

Say star A had an azimuth of 255˚ giving a PL of 165˚ - 345˚ and had an Intercept of 16.0’ Away

And star B had an azimuth of 135˚ giving a PL of 045˚ - 225˚ and had an Intercept of 24.0’ Towards

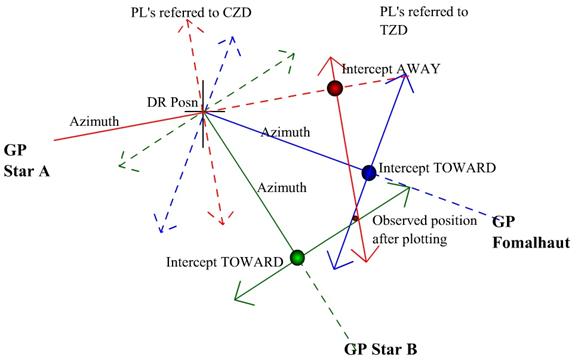
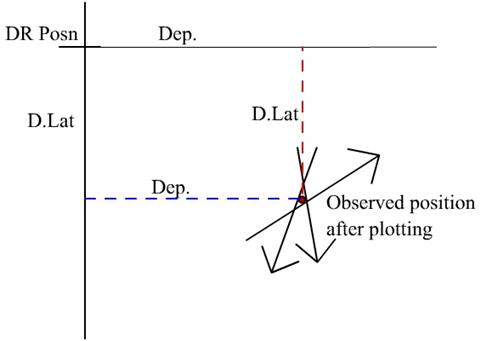
Apply the D.Lat to the DR Lat. To obtain the Observed Latitude

Use the Traverse Tables to get the D.Long for the measured Departure using the mean Lat.

Apply the D.Long to the DR Long. To get the Observed Longitude

IF THE STAR OBSERVATION CANNOT BE TAKEN AT THE SAME TIME AND THEY ARE OBSERVED WITH A LARGE INTERVAL OF TIME THEN RUN HAS TO BE APPLIED, ALL THE STARS HAVE TO BE WORKED WITH DIFFERENT DR’S AND THE PL OBTAINED WOULD HAVE TO BE SHIFTED TO THE MEAN TIME OF SIGHT AS SELECTED, TRANFEREING PL’S AS SHOWN EARLIER ON,