| Sailings | Chart Work Exercises | Information from Charts | Tides | Sextant |
Terrestrial Navigation
Definitions
THE SPHERE
The EARTH as a sphere is shown below.
In the following diagram of the Earth, two types of
circles (or rather half circles) have been depicted.
The Earth when cut up horizontally at the middle would
give rise to a circle of diameter equal to that of the Earth itself (assuming
that the Earth were a sphere). The Earth if cut up
anywhere else horizontally would produce circles which were smaller in diameter
than the central circle.
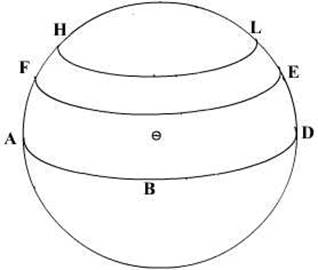
In the above ABD is the great
circle (maximum diameter), the Equator and the other circles FE and HL are
circles of smaller diameter than the equator.
These horizontal circles are called small circles.
They are the circles of latitude. Thus there is only one big circle equal to
the diameter of the Earth and that is at the middle of the Earth, the rest are
all, smaller than this circle. The circles are all parallel to each other, they are thus called the circles of Latitude or more
correctly the parallels of Latitude.
Thus small circles are circles on a sphere whose plane
does not pass through the centre of the sphere.
All circles of Latitude are small circles except the
Latitude of 0° - the equator.
If the Earth were to be cut vertically as depicted – then all the circles would have the diameter of the Earth. These circles are Great Circles. Thus all circles that equal the Earth’s diameter are called Great Circles and all that are smaller than the diameter of the Earth are called Small Circles.
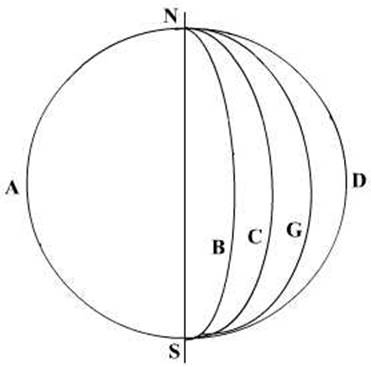
Great Circles are circles on a sphere whose plane
passes through the centre of the sphere.
The vertical Great Circles are called the circles of
Longitude, or more correctly they are termed the meridians of Longitude. The
vertical circles are thus not parallel to each other.
All meridians are great circles; the only horizontal
circle that is a great circle is the equator.
So now we have a method of defining a place on the
surface of the Earth. By quoting the circle of latitude passing over the place
as well as the vertical circle of longitude over the place, we may define its
position.
The vertical circles have all a common point of
intersection at the top and at the bottom of the Earth’s axis. These points are
called the poles of the circle.
A spherical angle is formed at the intersection
(giving rise to an angular difference) of two Great Circles.

Small circles: HKL
Great Circle: FBE, ABD
A spherical angle is equal to the plane angle that is
formed by the tangents to the great circles at their point of intersection.
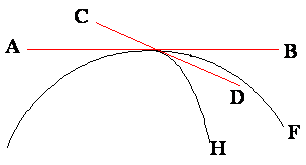
In the following figure, the triangle ABC is a
spherical triangle. It has been formed by the intersection of three great
circles. Great circles are those whose planes pass through the centre of the
sphere.

And a spherical triangle is formed when arcs of three
Great circles intersect to form a triangle.
The above angle and triangle do not follow the normal
triangular equations but they are governed by other equations.
Coordinates, termed latitude and longitude, can define
any position on earth.

Latitude (Lat.) is the angular distance from the
equator, measured northward or southward along a meridian from 0°at the
equator to 90°at the poles.
It is designated north (N) or south (S) to indicate
the direction of measurement.
The middle or mid-latitude (midLat.) between two
places on the same side of the equator is half the sum of their latitudes.
Mid-latitude is labelled N or S to indicate whether it is north or south of the
equator.
The expression may refer to the mid-latitude of two
places on opposite sides of the equator.
When the places are on opposite sides of the equator,
two mid-latitudes are generally used.
Calculate these two mid-latitudes by averaging one latitude and 0°
Longitude (Long.) is the angular distance between the
prime meridian and the meridian of a point on the earth, measured eastward or
westward from the prime meridian through 180°.
It is designated east (E) or west (W) to indicate the
direction of measurement.
Prime meridian
The meridian of
Today, all maritime nations have designated the
![]()
![]()
The difference of latitude (DLat.)
between two places is the angular length of arc of any meridian between their
parallels.
It is the numerical difference of the latitudes if the
places are on the same side of the equator; and
It is the sum of the latitudes if the places are on
opposite sides of the equator.
It may be designated north (N) or south (S) when
appropriate.
The difference of longitude (DLong) between two places
is the shorter arc of the parallel or the smaller angle at the pole between the
meridians of the two places.
If both places are on the same side (east or west) of
Greenwich, D.Long is the numerical difference of the longitudes of the two
places; if on opposite sides, D.Long is the numerical sum unless this exceeds
180°, when it is 360°minus the sum.
The distance between two meridians at any parallel of
latitude, expressed in distance units, usually nautical miles, is called
departure
(Dep.): It represents distance made good east or west
as a vessel proceeds from one point to another.
Its numerical value between any two meridians
decreases with increased latitude, while D.Long is numerically the same at any
latitude.
Either DLong may be designated east (E) or west (W)
when appropriate

Understanding
D.Lat.,
D.Long and Dep.
The above figure graphically shows the relation
between the above values.
In the sphere representing the Earth,
C is the centre of the Earth.
QABGQ’ is the Equator
DE and D’E’ describes the arcs of the small circles
ZDEJM and YD’E’KV which are parallels of Latitude
The arc AB on the equator is the difference of
Longitude between the position A and B on the equator.
The arc DE on the parallel of Latitude ZDEJM is the
Departure between the points D and E on the same parallel of Latitude.
Note that although the difference of Longitude between
D and E is the same as that of A and B, the distance as measured between them
is different.
The difference in the Latitude between the two small
circles is the difference in Latitudes.
The Earth as an Ellipsoid
Navigation is based upon the assumption
that the earth is a sphere and, consequently, on the laws of spherical
trigonometry. In reality, the shape of the earth is rather irregular and
approximates an oblate spheroid (ellipsoid) resulting from two forces,
gravitation and centrifugal force, acting on the viscous body of the earth.
While gravitation alone would force the earth to assume the shape of a sphere,
the state of lowest potential energy, the centrifugal force caused by the
earth's rotation contracts the earth along the polar axis (axis of rotation)
and stretches it along the plane of the equator. The local vector sum of both
forces is called gravity.
A number of reference ellipsoids are in
use to describe the shape of the earth, for example the World Geodetic System
(WGS) ellipsoid of 1984.
Earth data (WGS 84 ellipsoid):
Equatorial radius (Re) 6378137.0 m
Polar radius (Rp)
6356752.3142 m
Flattening ((Re – Rp) / Re)
1/298.25722
The values for polar radius and equatorial radius of
the earth, the great circle distance of 1' is 1.849 km at the poles and 1.855
km at the equator. This small difference does not produce a significant error
when plotting lines of position. It is therefore sufficient to use the adopted
mean value (1 nautical mile = 1.852 km).
However, when calculating the great circle distance of
two locations thousands of nautical miles apart, the error caused by the
flatness of the earth can increase to several nautical miles.
Distance:
The Nautical Mile is the arc of the earth’s
circumference subtended by an angle of ONE MINUTE at the centre of curvature.
The varying curvature of the earth makes the length of a minute of arc at the
surface vary slightly with the Latitude so that the nautical mile measures 6108
feet at the poles where the curvature is flatter and 6048 feet at the equator
where the earth’s curvature is sharper.
A mean length of 6080 feet is universally adopted in
navigation.
The Cable is the tenth part of a nautical mile. It is
customary to declare a cable as 600 feet and this is used for navigational
purposes irrespective of Latitude.
A Knot is a unit of speed (no definite directional
vector) or velocity, represents a speed of ONE
NAUTICAL MILE PER HOUR.