Back to Nautical	Definition	Charts	Rotation of the Earth	Distances	Position Lines
	Sailings	Chart Work Exercises	Information from Charts	Tides	Sextant

Terrestrial Navigation

Chartwork Exercises

Distance

Distance, as used by the navigator, is the length of the rhumb line connecting two places. This is a line making the same angle with all meridians. Meridians and parallels, which also maintain constant true directions, may be considered special cases of the rhumb line. Any other rhumb line spirals toward the pole, forming a loxodromic curve or loxodrome.

Distance along the great circle connecting two points is customarily designated great-circle distance. For most purposes, considering the nautical mile the length of one minute of latitude introduces no significant error.

Heading

Heading (SH) is the direction in which a vessel is pointed, expressed as angular distance from 000˚clockwise through 360˚.

Do not confuse heading and course.

Heading constantly changes as a vessel yaws back and forth across the course due to sea, wind, and steering error. While the course to be steered or steered is constant.

Bearing (Brg.) is the direction of one terrestrial point from another, expressed as angular distance from 000˚(North) clockwise through 360˚. When measured through 90˚or 180˚from either north or south, it is called bearing angle (B). Bearing and azimuth are sometimes used interchangeably, but the latter more accurately refers to the horizontal direction of a point on the celestial sphere from a point on the earth. A relative bearing is measured relative to the ship’s heading from 000˚(dead ahead) clockwise through 360˚. However, it is sometimes conveniently measured right or left from 0˚at the ship’s head through 180˚.

This is particularly true when using the table for Distance of an Object by Two Bearings.

To convert a relative bearing to a true bearing, add the true heading:

True Bearing = Relative Bearing + True Heading.

Relative Bearing = True Bearing – True Heading.

Relative bearings are sometimes termed RED (0° to 180°) for port and GREEN (0° to 180°) for starboard.

For example: On a course of 125°T and the ships bridge wing repeaters not working, the bearing may still be taken – by using the PELORUS ring.

A object is selected and the relative bearing is read on the brass ring, the bearing may be 30° on the port side of the Fore and aft line of the ship. It is then called as RED 30°.

To convert: True Bearing = Ships Head - 30°

= SH - 30° or 125 – 30 = 095°T

Similarly if the object were on the starboard side of the fore and aft line of the ship, then with the same bearing it would be called as GREEN 30°, to convert:

True Bearing = Ships Head + 30°

= SH + 30° or 125 + 30 = 155°T

Set and Drift

Set refers to the current’s direction, and drift refers to the current’s speed.

Leeway is the leeward motion of a vessel due to that component of the wind vector perpendicular to the vessel’s track.

Leeway and current effects combine to produce the most pronounced natural dynamic effects on a transiting vessel.

In addition to these natural forces, helmsman error and gyro error combine to produce a steering error that causes additional error in the DR.

Calculating Set And Drift And Plotting An Estimated Position

It is difficult to quantify the errors discussed above individually. However, the navigator can easily quantify their cumulative effect by comparing simultaneous fix and DR positions. Were there no dynamic forces acting on the vessel and no steering error, the DR position and the fix position would coincide. However, they seldom coincide. The fix is offset from the DR by a finite distance.

This offset is caused by the error factors discussed above.

Note again that this methodology provides no means to determine the magnitude of the individual errors. It simply provides the navigator with a measurable representation of their combined effect.

When the navigator measures this combined effect, he often refers to it as the “set and drift.” Recall from above that these terms technically were restricted to describing current effects. However, even though the fix-to-DR offset is caused by effects in addition to the current, here it is assumed the offset as the set and drift.

The set is the direction from the DR to the fix. The drift is the distance in miles between the DR and the fix divided by the number of hours since the DR was last reset. This is true regardless of the number of changes of course or speed since the last fix. Calculate set and drift at every fix.

Leeway:

Leeway is the effect of the wind on the course of a ship.

A ship sails along a course line from point A towards point B, if there were no wind and no current then the ship would be at point B after a certain amount of time.

However if there is some wind and that affects the ship in keeping her course then she would be sailing a slightly different course. The effect would be that she would be off her destination point either in time or in distance away.

To find out and allow leeway:

Face in the direction of the ships heading, and if the wind is from the right side then the leeway to be applied is to the left.

Leeway is termed (+) when the wind is to the Port side of the ship and (-) when the wind is on the starboard side of the ship

Estimated Course And Speed Made Good

The direction of a straight line from the last fix to the EP is the estimated track made good. The length of this line divided by the time between the fix and the EP is the estimated speed made good.

Measuring Courses And Distances

To measure courses, use the chart’s compass rose nearest to the chart section currently in use. Transfer course lines to and from the compass rose using parallel rulers, rolling rulers, or triangles.

The navigator can measure direction at any convenient place on a Mercator chart because the meridians are parallel to each other and a line making an angle with any one makes the same angle with all others. Measure direction on a conformal chart having nonparallel meridians at the meridian closest to the area of the chart in use. The only common non-conformal projection used is the gnomonic; a gnomonic chart usually contains instructions for measuring direction.

Compass roses give both true and magnetic directions.

For most purposes, use true directions.

Measure distances using the chart’s latitude scale. Assuming that one-minute of latitude equals one nautical mile introduces no significant error. Since the Mercator latitude scale expands as latitude increases, measure distances on the latitude scale closest to the area of interest. On large scale charts, such as harbour charts, use the distance scale provided.

To measure long distances on small-scale charts, break the distance into a number of segments and measure each segment at its mid-latitude.

Navigational computers can also compute distances between two points. Because of the errors inherent in manually measuring track distances, use a navigation computer if one is available.

Fixing the ship using only bearings

Doubling The Angle At The Bow

The basis of this method is to take advantage of geometry – an isosceles triangle.

The bearing of a point is noted preferably fine on the bow, the angle is doubled and a wait ensues, as the vessel proceeds along her course, the time that the point bears the double of the 1^st bearing is noted.

Then the distance traveled during the time period from 1^st bearing to the time of the 2^nd (double the angle) bearing is the distance that the vessel is off the point at the time of the 2^nd bearing.

Further calculation will give the beam distance,

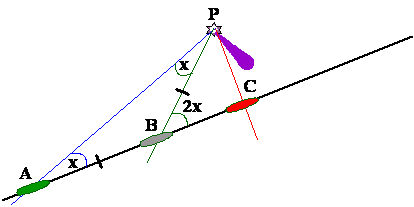
In the above figure, the position of the ship when she takes the 1^st bearing is A, at the 2^nd position it is B and when abeam the ship is at C.

The angle at A is half that of the angle at B, this gives that the distance BP = AB the distance run by the ship.

Knowing the angle at B and the side BP, we can find the distance when abeam PC.

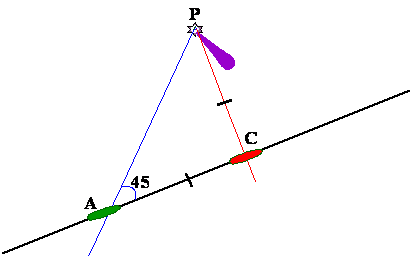
Another method – Four Point Bearing:

In this the above exercise is carried out with a difference. The difference being that the 1^st angle is 45˚ (four points) and the 2^nd bearing is 90˚ (double of the 1^st bearing),

But 90˚ on the bow is also the beam distance, thus it gives the beam distance as the distance run between the 1^st and the 2^nd bearings. The only disadvantage in this is that the beam distance is known when the vessel is actually abeam.

However it does help since it gives and indication of the distance that is going to be when abeam by the time that is elapsed between the 1^st and the 2^nd bearings.

Running Fix:

In this case only one object is used to obtain the vessel’s position, though not an accurate one.

Used when only one prominent object is available for fixing the position of the vessel.

Today with the advent of Radar navigation, this method is rarely used. However in case both the radar’s fail, and the navigator has to rely on fixes (visual) to navigate then the above would come in handy.

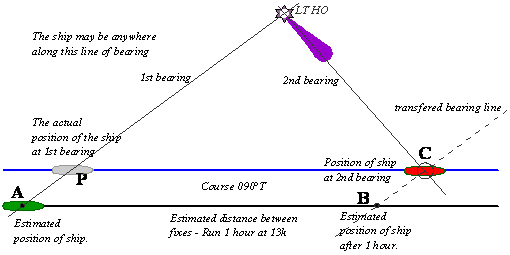
In the above figure, the ship has a Light House in view and takes a bearing at 0800hrs.

She then proceeds on her course of 090°T for a period of 1 hour at a speed of 13knots.

Thus the distance covered is 13NM.

She thus starts from the position A and arrives at position B after doing 13NM.

The first bearing is transferred to B and a new bearing is taken, where both intersect is the position of the ship. If we now draw a line parallel to the course line from the actual position of the ship at 2^nd bearing, C, then the 1^st actual position would be the point P.

If there is a current being experienced then the entire estimated course and the distance traveled will have to be first deduced and then the above may be done.

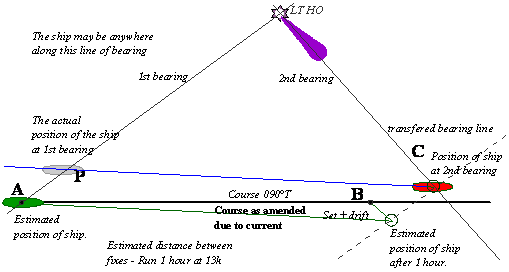
Draw the course line from A to B; allow the set and the drift of the current at position B.

Then this would be the estimated track of the ship after this the 1^st and the 2^nd bearing parts become as described earlier.

There are some special angles which give the distance off that a ship will pass when abeam of a point, however the number of such special angles are limited and the student is asked to refer to – Nicholls’s Concise Guide for further reading.

Sextant Angles:

Before the advent of Radar, the sextant was a handy instrument from taking celestial angles to taking terrestrial angles. The sextant was used to find the distance off from lighthouses as well as for fixing the position of the ship without using the compass.

For finding the distance off from Lt Houses and high conspicuous hilltops the vertical sextant angle was used in conjunction with a bearing fixed the position of a ship.

The horizontal sextant angle was used when two or more prominent points were available and the position of the ship was fixed without using a bearing.

Vertical Sextant Angle:

The angle subtended by the top and bottom of the object at the observer is noted and the angle is corrected for Dip and IE.

The corrected angle is then used with the height of the object to obtain the distance off from the object.

The expression used is:

_{Distance Off in NM =} Height of the object in feet x 0.565

Vertical sextant angle in minutes

Horizontal Sextant Angles:

For use in position fixing without the aid of a compass.

Three conspicuous points are selected, ensure that the angles that they subtend are wide.

The sextant is held horizontally and the sextant angle between point A and point B is obtained.

Then the sextant is used to obtain the angle between points B and C.

Straight lines are drawn between points A to B, and again between points B to C.

Say the angle obtained between A and B is 58°, therefore the complement is 32°, (90-58)

Also say the angle obtained between B (2^nd instance) and C is 42°, therefore the complement is 48°, (90-42)

Using the parallel ruler lines are drawn with the complement angles from the respective points.

Point A: 32° and point B: 32° - first position circle

Point B: 48° and point C: 48° - second position circle

Case 1

The intersection of the complement lines from A and B intersect at point P, this would be the centre of the position circle, touching the points A and B and the ship is on this circle.

Case 2

The intersection of the complement lines from B (2^nd instance) and C intersect at point Q, this would be the centre of the position circle, touching the points B and C and the ship is on this circle.

The point of intersection of the two circles is then common and so the ship is at that position.

Visibility of Lights:

Lights are placed on Light Houses at a height of the light houses, depending on the intensity of the lights themselves, the lights are marked as visible up to a distance of a certain limit, the height of the observer when declaring the above is taken to be 15 feet.

However the visibility of the lights at the marked limit may be exceeded due to the height of the ship also.

The expression for obtaining the raising of the light limit is given by:

Heights in feet

Distance = (√Height of observer x 1.15) + (√Height of Object x 1.15)