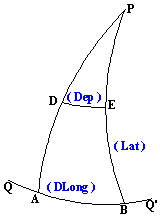Terrestrial Navigation
Sailings
OBTAINING
VESSELS POSITION USING CELESTIAL OBSSERVATIONS
Position finding at sea by the methods of nautical
astronomy depends upon the solution of an oblique spherical triangle, and
practice in the application of the formula is essential in order to acquire
facility in its manipulation.
In the following figure, the triangle
ABC is a spherical triangle. It has been formed by the intersection of three
great circles. Great circles are those whose planes pass through the centre of
the sphere.
ABD, ACP and BCE are three great circles, and
triangles ABC and DCB are two of the spherical triangles formed by their
intersection. All the angles at A, B and C are spherical angles.
As has been stated before the sides of a spherical
triangle are measured and expressed in angular notation instead of in distance
units. However on the surface of the Earth, the sides are converted from the
angular measurement into the distance unit by multiplying with the length of
the ONE-MINUTE of the arc, that is 1853 nautical
miles.
The chief
properties of a spherical triangle are:
The sides are expressed in angular measure
The sum of all the angles in a spherical triangle is
equal to a figure between 180° to 540° or between 2 right angles to six right
angles.
The sum of the three sides of a spherical triangle
must be less than 860°
As with plane triangles the greatest side is opposite
to the greatest angle.
Where 2 great circles cut each other the vertically
opposite angles are equal.
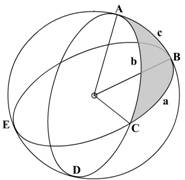
In the above figure, we have the angles as A, B and C,
the sides corresponding to the angles would be a, b and c
The formula used to calculate an angle or a side is
given by:
hav A = hav a hav (b~c)
sin b x sin c
In the above formula the expression hav (b~c) indicates that the result should always be positive. In case b is greater than c, then c will be subtracted from b, and
vice versa. The symbol ~ indicates difference.
In the above we have tried to find the angle A,
however if the angle required is B then the formula has to be replaced by the
known figures.
hav B = hav b hav (a~c)
sin a x sin c
The formula would again have to be amended if any of
the sides are required.
Solution Of
Right Angled Spherical Triangles
A rare triangle since it is not always possible to get
a right angled spherical triangle.
The right-angled spherical triangle may be solved
using the haversine formula as described above but may also be solved easily
using Napiers Rules for Circular Parts.
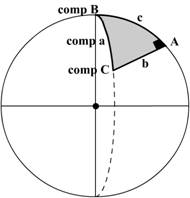
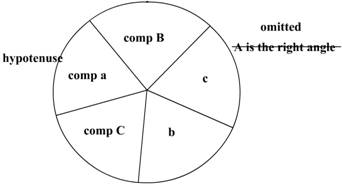
In the above figure the right angled spherical
triangle is shown, the hypotenuse and the other sides are indicated.
The rules
are thus:
A triangle has six parts the three sides and the
three angles. However using Napiers Rule the 5 parts are used, the right angle
is omitted.
The complements of the hypotenuse and the two angles
are used. Complement means that the angles have to be subtracted from 90° and
then used. However instead of subtracting from 90° we may also use the
following:
sine (90°-
Angle) = cosine angle
tangent (90° -
angle) = cotangent angle
Adjacent part means the immediate next part. Opposite
means the part next to an adjacent part.
If any of the three parts is selected as a mid part,
the other two must be either adjacent parts or opposite parts. This depends on
which formula is used as stated below:
Sine
of middle part = product of tangents of adjacent parts
OR
Sine
of middle part = product of cosines of opposite parts.
Filling up the circular part, start from any angle or
side and proceed in a clockwise direction similar to the triangle itself.
REMEMBER THAT THE COMPLEMENTS ARE USED OF THE
HYPOTENUSE AND THE TWO ANGLES THE RIGHT ANGLE IS OMITTED.
THERE ARE FIVE PARTS AND NOT SIX.
Sailings
The compass was developed about 1000 years ago.
However it was not until the 1870s that Lord Kelvin developed a reliable dry
card marine compass. The fluid-filled compass became standard in 1906.
Variation was not understood until the 18th century,
when Edmond Halley led an expedition to map lines of variation in the South
Atlantic. Deviation was understood at least as early as the
early 1600s, but correction of compass error was not possible until Matthew
Flinders discovered that a vertical iron bar could reduce errors. After 1840,
British Astronomer Royal Sir George Airy and later Lord Kelvin developed
combinations of iron masses and small magnets to eliminate most magnetic
compass error.
The gyrocompass was made necessary by iron and steel
ships. Leon Foucault developed the basic gyroscope in 1852. An American (Elmer
Sperry) and a German (Anshutz Kampfe)
both developed electrical gyrocompasses in the early years of the 20th century.
Coordinates, termed latitude and longitude, can define
any position on earth.
Latitude (Lat.) is the angular distance from the
equator, measured northward or southward along a meridian from 0°at the
equator to 90°at the poles.
It is designated north (N) or south (S) to indicate
the direction of measurement.
The difference of latitude (DLat.)
between two places is the angular length of arc of any meridian between their
parallels.
It is the numerical difference of the latitudes if the
places are on the same side of the equator; and
It is the sum of the latitudes if the places are on
opposite sides of the equator.
It may be designated north (N) or south (S) when
appropriate.
The middle or mid-latitude (midLat.) between two
places on the same side of the equator is half the sum of their latitudes.
Mid-latitude is labeled N or S to indicate whether it is north or south of the
equator.
The expression may refer to the mid-latitude of two
places on opposite sides of the equator.
When the places are on opposite sides of the equator,
two mid-latitudes are generally used.
Calculate these two mid-latitudes by averaging each
latitude and 0°
Longitude (Long.) is the angular distance between the
prime meridian and the meridian of a point on the earth, measured eastward or
westward from the prime meridian through 180°.
It is designated east (E) or west (W) to indicate the
direction of measurement.
The difference of longitude (DLong) between two places
is the shorter arc of the parallel or the smaller angle at the pole between the
meridians of the two places.
If both places are on the same side (east or west) of
Greenwich, DLong is the numerical difference of the longitudes of the two
places; if on opposite sides, DLong is the numerical sum unless this exceeds
180°, when it is 360°minus the sum.
The
distance between two meridians at any parallel of latitude, expressed in
distance units, usually nautical miles, is called departure
(Dep.). It
represents distance made good east or west as a vessel proceeds from one point
to another.
Its numerical value between any two meridians
decreases with increased latitude, while Dlong. is numerically the same at any latitude.
Either DLong. may be designated east (E) or west (W) when appropriate.
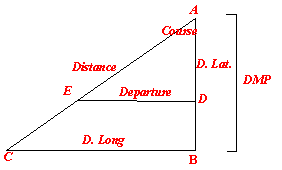
Distance
Distance, as used by the navigator, is the length of
the rhumb line connecting two places. This is a line making the same angle with
all meridians. Meridians and parallels, which also maintain constant true
directions, may be considered special cases of the rhumb line. Any other rhumb
line spirals toward the pole, forming a loxodromic
curve or loxodrome.

AB and DE are arcs of concentric circles, if viewed
from the poles, their centres F and C being on the earths axis, and as arcs of
circles are proportional to their radii, thus we have:

The value that is required may be now found using the
above formula and transposing as required.
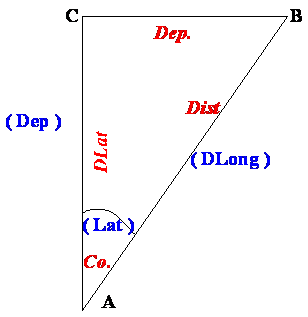
In the above simple right angled plane
triangle, the Blue Regular font indicates the factors used in the same triangle
in the Travers Tables for using in Parallel sailing problems.
The Red Italics font indicates the factors used in the
Traverse Tables for solving problems in Plane sailing.
In PLANE SAILING the
angle is made equal to the Course.
The hypotenuse is made equal to the Distance.
The side adjacent to the angle is made equal to the D.
Latitude.
And the side opposite to the angle is made
equal to the Departure.
In PARALLEL SAILING the angle is
made equal to the Latitude.
The hypotenuse is made equal to the D.
Long.
And the side adjacent to the angle is made equal to
the Departure.
The Traverse tables are a combination of
the two tables as above, the navigator must be careful to select the correct
table. The entries are as described above. The Italics and Regular font play an
important part in differentiating the Tables.
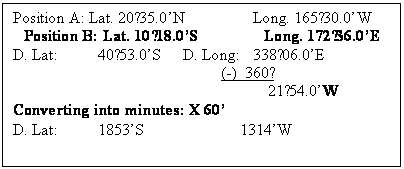
Finding the Difference in Latitude (D.Lat.)
and the Difference in Longitude (D.Long).
(Before proceeding with examples in
parallel sailing problems)
D. Lat.: Subtract the two latitudes if
they have the same names.
Add
if the two Latitudes have different names.
The naming convention is Northerly D.Lat if more North and Southerly if more South.
Once the D.Lat
in degrees and minutes has been found out convert the same into minutes. D.
Lat is then used as minutes.
D. Long: Subtract the two Longitudes if
they have the same names.
Add
if the two Longitudes have different names.
The naming convention is Easterly D. Long if more East
and Westerly if more
West. If the sum of a East longitude or a West
longitude exceed 360˚, then the same is subtracted from 360˚ and the
name is reversed.
Once the D. Long in degrees and minutes
has been found out convert the same into minutes. D. Long is then used as
minutes.
PARALLEL SAILING
As explained before the factors are:
Latitude, D. Longitude and the Departure
Parallel sailing as stated above has lost
its prominence in navigation. This type of sailing is no longer practiced, however it is still used for finding out the mean
distance traveled between two meridians.
Used for distances less than 600 NM, the
parallel sailing formula is used with a difference.
The Latitude used is that of Mean between
the two positions.
So
now the formula stands amended to:
Dep. = D. Long x cos. Mean Latitude.
As long as the difference between the
Latitudes is small, Mean Latitude used is sufficient, however if the Difference
of Latitude is large then, Middle Latitude is used.
Mean Latitude is the arithmetical mean of
the two latitudes, but Middle Latitude takes into account the convergence of
the earth.
Middle Latitude is the Latitude on which the actual Departure
lies.
This
convergence correction is obtained from the nautical Tables.
Knowing the departure we can now find the
Course and the Distance.

Mercator Sailing gives accurate results
for long distances, more so when there is a very large change in the Latitude
between the two positions.
Finally:
Mercator Sailing: Course D. Long. DMP
(difference in Meridional Parts)
Parallel Sailing: Mid.
Lat. D. Long. Dep.
Plane Sailing: Course Distance Dep. D. Lat.
The connections:
D. Long. Connects Mercator to Parallel
Sailing
Departure connects Plane with Parallel
Sailing
Course connects Mercator with Plane
Sailing.
Using the above we can find out the set
and drift of the current, or knowing the set and drift of the current we can
find our DR position. This is useful if we have to make a rendezvous with
another vessel in a search and rescue operation.
DR Posn.:
Lat.: 50°20.0N Long.: 115°37.0E
Obs.
Posn: Lat.: 50°40.0N Long.: 115°20.0E
To find the
set and drift.
DR Posn.:
Lat.: 50°20.0N Long.: 115°37.0E
Obs.
Posn: Lat.: 50°40.0N Long.: 115°20.0E
D. Lat: 00°20.0N D. Long: 00°17.0
Use Traverse Tables:
M. Lat.: 50°30.0
& D. Long
Gives a Dep.: 10.8
Entering
with D. Lat & Dep.
Gives: Course: 28°
Distance: 23
So the set would be N28°W
and the Drift would be: 23NM
|
|

The Meridional Parts for any latitude is
the increased length of the meridians on a Mercator chart measured from the
equator to the parallel and expressed in minutes of the Longitude scale.
Example: The length of the meridian A to D
when measured along the equator represents the number of meridional
parts corresponding to ad; and AE to ae; AF to af
and so on.
If position d is Latitude 30°N, then the
measured as a line distance on the earths surface of ad is 30° x 60 = 1800NM,
but on referring to the Meridional Parts table in the Nautical Tables the MP
for 30° is 1877, so the meridional distance AD on the
chart is 77 equatorial minutes longer than on the globe.
Difference
Of Meridional Parts:
Is the difference between the MP of two Latitudes.
Using MP the factor Departure disappears
and is replaced by D. Long.
In the same equation Latitude also
disappears and is replaced by DMP.
So on
the Mercator chart we would have:

The
Navigational features of a Mercator Chart are:
The world, with the exception of the
higher Polar Regions,
can be seen at a glance
The rhumb line track from one position to
another is a straight line
The great circle track from one position
to another is an arc.
The course from one position to another
can be read by using a parallel ruler and playing it to the compass rose and
reading the course directly.
The scale of the Latitude at the side of
the chart is also the scale for distance in nautical miles. Note however that
if the positions are separated by a considerable difference in Latitude then
the divider for measuring the distance should be placed at the mean latitude or
they will be a discrepancy.
Calculating the course and distance
between two places is reduced to solving a plane right-angled triangle.
The Great Circle track is the shortest
distance between two places. (When a crow flies or when a person is traveling
between two points that are visible on the earths surface but separated by
some distance, the person makes a GC track.)
However if sailing on a Mercator chart and
following a GC track the course line would be a curve as such the vessel would
have to be continually altering course, this because the track is crossing the
meridians at a different angle. (An aircraft pilot on the other hand when he
does visual navigation instead of following a charted course line is doing a GC
track).
The GC track bends towards the Pole, so on
a East-West course the course line would initially be NE then E after passing
the vertex the course would become slowly SE.
Since the course cannot be continually
altered, an alternate method is chosen. The course line is laid on a Gnomonic
Chart, where the GC track would appear as straight line.
From this the alteration points are
decided, say at every 10° of longitude, the co-ordinates (Latitude and
Longitude) of these points are taken and are transferred to a Mercator Chart.
And the ship then sails a rhumb line track
between the selected parts of th4e track, altering as and when she reaches the
alteration points.
Mercator
Sailing:
The above calculations are resorted to
when a distance of more than 600NM separates the two positions.
Example:
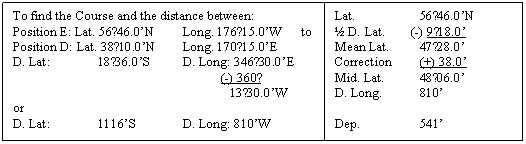
To find the Course and Distance between:
Posn
A: Lat.: 49°58.0N MP:
3453.43 Long.: 005°12.0W
Posn
B: Lat.: 37°49.0N MP:
2439.97 Long.: 025°08.0W
For the calculation we add a
column for MP
A: Lat.: 49°58.0N MP: 3453.43 Long.: 005°12.0W
B: Lat.: 37°49.0N MP: 2439.97 Long.: 025°08.0W
D. Lat.: 12°09.0 DMP: 1013.46 D. Long.: 19°56.0
D. Lat.: 729 D.
Long.: 1196
In the triangle ABC we
have: B = 90°, AB = DMP,
BC = D. Long
We have to find A
the course steered.
Tan course =
D. Long = 1196
DMP 1013.5
Course = 49°43.3 or S49°43.3W or 229°43.3
|
|
|
|
Once the Course is
obtained, we use the course to find the distance sailed.
AD = D. Lat = 729
A = 49°43.3
D = 90°
In the triangle ADE:
AE = AD x sec. A or
Distance = D. Lat. x secant A
Or = 729 x sec. 49°43.3
Distance = 1128NM
|
|
NOTE: THE LINE AC IS NOT THE DISTANCE FROM POSITION.
A, TO POSITION B, IT IS SIMPLY A RHUMB LINE TO COMPLETE THE TRIANGLE.
From the above example, if we plot the
factors, we would obtain 2 right-angled triangles. They both have in common are
the Course and the distance steamed.
The above shows how the two equations may
be merged to get the course and the distance between two points.
GREAT CIRCLE SAILING
Due to the Earth being almost a
sphere the shortest distance as measured on the Earths surface would be a
straight line that would curve with the curvature of the Earth.
Since all navigation is however
done on a Mercator chart which has been designed to show the surface of the
Earth as a flat piece of paper the straight line that is drawn on the chart
is not a straight line on the surface of the Earth.
There lies therefore a difference
in the planning of the sailing on paper and the final sailing itself which is
done on the surface of the Earth.
For short distances and sometimes
for convenience the plane and parallel sailing is utilized, however when
undertaking long trans Pacific or Atlantic sailings a
great circle route reduces the distance by an appreciable amount.
Due to the nature of the Mercator
chart a great circle course (straight line on the surface of the Earth) is
produced as a curve. Again a difficulty arises as to how to draw the curve.
Therin comes the
requirement of the calculation of the Great circle track the initial course
the final course and the overall distance. Once these are found out the nest
step is to follow this curved course line on a Mercator chart. Obviously a ship
cannot keep altering her course to follow the curve so a
interval of say 10° is adopted
and the curve is broken up into a series of short straight lines on the
Mercator chart, these short straight lines would follow the curve as much as
possible.
If however a gnomonic chart (the
chart is as if it has been peeled off from the surface of the Earth the poles
are as they should be) is available on board then the great circle track may be
drawn as a straight line from the initial position to the final position. This
line as already explained would be a curve on the Mercator chart.
As discussed earlier the interval
of 10° is adopted
and the points of alteration of course is lifted from the gnomonic chart and
the positions are transferred to the Mercator chart and the straight lines are
joint to the points so obtained (at intervals of 10°). Thus a modified curve is
finally sailed on.
All calculation of the initial
course, final course as well as the distance between poits
A and B are resolved using the haversine formulae for spherical triangles. Since on the surface of the Earth the sides of the triangle are
made up of great circles.
Thus, the formula used is:
Haversine (one side) = haversine
(opposite angle) x sine (adjacent side) x sine (adjacent side) + haversine
(difference between adjacent sides).
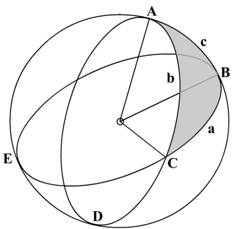
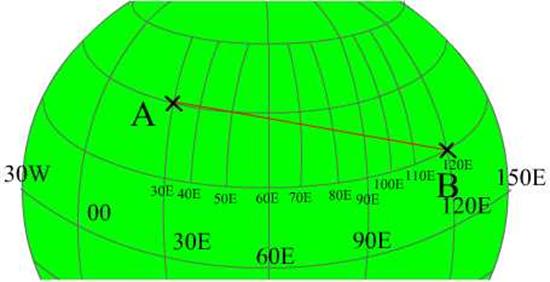
Coming to and example:
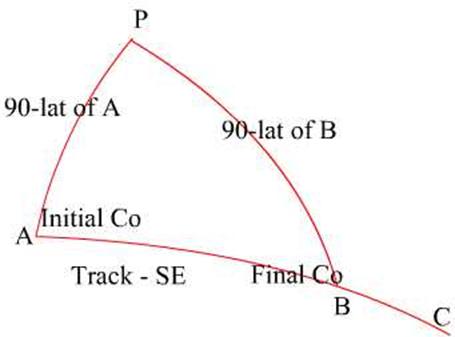
In the above triangle the
distance as required is from point A to point B.
So,
Hav AB = hav P x
sin PA x sin PB + hav (PA-PB)
Where PA is the meridian passing
through point A and PB is the meridian passing through B and AB is the
intended track.
Let us assume that point A and B
have the following co-ordinates:
|
|
Latitude
|
Longitude
|
|
Initial: A
|
20°00N
|
030°00E
|
|
Final: B
|
10°00N
|
120°00E
|
|
Difference
|
10°00N (d.lat)
|
90°00E (d.long)
|
Since the travel from A to B is
eastwards the difference is East, the naming is
irrespective of the longitude it depends only on the track direction.
Therefore: Hav AB = hav P x
sin PA x sin PB + hav (PA-PB)
PA is co-lat of A = (90-20) = 70°, and PB is the co-lat of B
= (90-10) = 80°
Inserting the values to the
equation:
Therefore: Hav AB = hav P x
sin PA x sin PB + hav (PA-PB)
Hav AB = hav
(d.long) x sin (90-lat of A) x sin (90-lat of B) + hav (d.lat)
Hav AB = hav 90° x sin 70° x sin 80° + hav 10°
AB = 86°35.7 equates to a distance
of 5195.7 NM
Calculating the Initial course for
the above example:
We now have the triangle PAB with
all the three side values and the value of the angle P.
It thus becomes easy to apply the
haversine formula to get the other values.
To find the initial course we have
to find the value of angle at A (angle PAB), using the formula:
Haversine of one angle = cosecant
adjacent side x cosecant adjacent side x (haversine opposite side haversine
difference between the adjacent sides)
Or applying
to our figure:
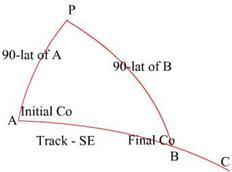
Hav A = cosec PA (cosecant adjacent side to A) x cosec AB (cosecant adjacent side to A) x [hav PB (haversine opposite side to A) hav (PA~AB) {haversine difference between the adjacent sides}]
Hav A = cosec PA x cosec AB x [hav
PB hav (PA~AB)]
Inserting the values:
Hav A = cosec 70 x cosec 86°35.7 x [hav 80 hav (86°35.7-70)]
Hav A = cosec 70° x cosec 86°35.7 x hav 63.4°
A = 80°35.5SE equates to 099°24.5 = Initial Course
Calculation of the Final Course:

The Final Course is the angle PBC, so
in order to get that angle we would have to find the angle PBA and then
subtract or add 180°
to it.
Thus by haversine formula we need to obtain the angle
PBA.
Again:
Hav B = cosec PB (cosecant adjacent side to A) x cosec AB (cosecant adjacent side to A) x [hav PA (haversine opposite side to B) hav (PB~AB) {haversine difference between the adjacent sides}]
Hav B = cosec PB x cosec AB x [hav
PA hav (PB~AB)]
Inserting the values:
Hav B = cosec 80 x cosec 86°35.7 x [hav 70 hav (86°35.7- 80)]
Hav B = 70°16.8 equates to 109°43.2 = Final Course
Composite great circles
We have previously calculated distances using the
great circle method, no doubt there would be a great saving in distance. But
what happens if the Great Circle track takes a ship to extreme high latitudes
where the weather associated with the latitude is too cold and too rough?
To escape such weather the idea is to sail part of the
way on a Great Circle track and then sail along a parallel and then again do a
Great Circle sailing until the destination point is arrived at. This type of
sailing is known as Composite Sailing.
So how is this done?
The initial position is taken and the vessel sails up to the latitude of the Vertex and then sails along
the parallel of latitude of the Vertex and then after sailing thus sails down
to the final point in a Great Circle track.
This brings up Vertex.
Vertex of a great circle as stated above is the point
where the Great Circle reaches its maximum latitude that the vessel has decided
on.
A Great
Circle would have 2 Vertexs, 180° apart. That is one in
either hemisphere.
A Great
Circle track extended to cut the equator
at any point would have a difference of longitude of 90° between that point and the
Vertex.
For a Great Circle as the Great Circle goes away from
the equator the North or the South component of the track progressively reduces
and the East or West component keeps increasing. This is so until the Vertex is
reached where the North or South component completely disappears and the East
or the West component is the only one present.
After the vertex the track slowly gains the North or
South component and loses the East or West component until the equator.
The Vertex gives warning of the extreme latitude that
the vessel may reach while sailing the Great Circle track. So during planning
the track may be modified to complete the sailing on favourable maximum
latitude. The position of the Vertex also eases the calculation of the
intermediate position of the track (as decided for using the track on a
Mercator Chart).
Position of the Vertex:
01. Vertex is
in the same hemisphere if both the Initial and the Final positions are in the
same hemisphere.
02. Vertex is
in the hemisphere of the higher latitude (between the Initial and Final points)
if they lie in separate hemispheres.
03. The Vertex
lies between the Initial and the Final points if both the points are in
different quadrants (NESW).
04. However if
the Initial and the Final points are both in the same quadrant then the Vertex
would lie on the extended track joining the two, either towards the Initial
point or towards the Final point.
In the example used until now the Vertex would be as
such:
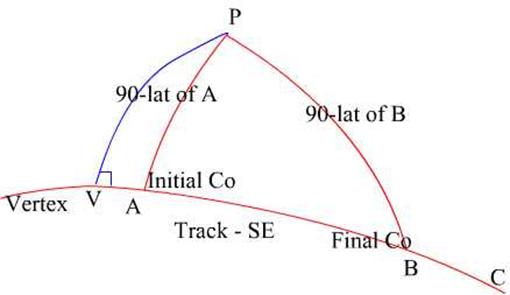
Consider the triangle PAV, where the
point V is the Vertex and a right angled spherical triangle, since PV is the
meridian of V. The course line would be East or West in the example it is Easterly.
Then using Napiers rule:
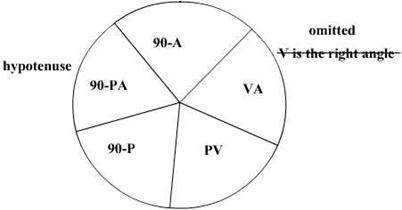
To find the latitude of the Vertex:
From Napiers Rule:
Sine of mid part = cosine of opposite parts or
Sin mid part = cos opp part
x cos opp part
Sin PV = cos (90 A) x cos (90 PA)
Sin PV = cos (90 - 80°35.5) x cos (90 70)
PV = 67°59 or the Latitude of the Vertex is 22°01N
To find the
Longitude:
Sin mid part = tan adj part
x tan adj part
Sin (90 - PA) = tan (90 - A) x tan (90 - P) or
Tan (90 P) = sin (90 PA) x 1/ tan (90-A)
Tan (90 P) = sin (90 70) x 1/ tan (90 - 80°35.5)
Tan (90 P) = tan P = 64°09.2West of A, therefore
the Longitude of the Vertex would be: 034°09.2W
Now to move on to Composite Great Circle sailing,
Point to remember is that there are actually 2 Great
Circles, one for the initial course and upto the Vertex latitude and then there
is parallel sailing along the latitude of the Vertex and then there is the
other Great Circle which would bring the vessel to the destination the final
course.
Basically since the Great circles have been separated
and one part of the triangle is a right angled triangle (due to the Vertex) the
entire exercise is done using Napiers Rule and so is
less time consuming.
The figure shows the two Vertexs of the two Great
Circles, and the parallel track between the two Vertexs.
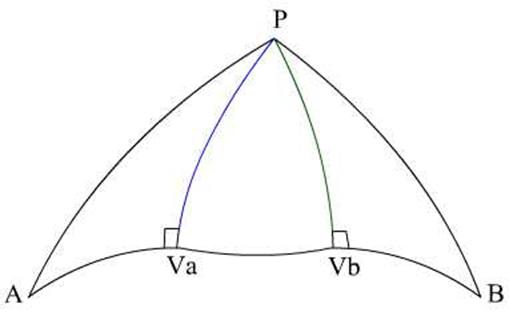
Given a vessel would like to have the maximum latitude
during a Great Circle passage to be 55°N. Given that the vessel would depart from position:
|
|
Latitude
|
Longitude
|
|
Initial A
|
49°°00N
|
030°00E
|
|
Final - B
|
50°00N
|
120°00E
|
|
Difference
|
|
90°00E (d.long)
|
Using Napiers Rule

|
Lat A
|
49N
|
|
PB
|
40°
|
|
Lat B
|
50°
|
|
|
Lat Va
|
55N
|
|
PW
|
35°
|
|
PB
|
40
|
|
|
PA
|
41°
|
|
|
|
|
|
|
|
|
PV
|
35°
|
|
|
|
|
|
|
|
In the first right angled spherical triangle PAVa
Sin A = cos lat Va x Sec lat
A
Sin A = cos 55° x sec 49°
A = 60°57.6
Initial Course
Again for the distance AVa:
Cos AVa = sin lat A / sin lat Va
Cos AVa = sin 49 / sin lat 55
AVa = 1372.7 NM
In the final right angled triangle PBVb:
Sin B = cos lat Vb x Sec lat B
Sin A = cos 55° x sec 50°
A = 116°10 Initial Course
Again for the distance AVb:
Cos AVb = sin lat B / sin lat Vb
Cos AVb = sin 40 / sin lat 55
AVb = 2298 NM
Once the Great Circle tracks have been covered, the
parallel sailing track has to be calculated that is the distance between Va to Vb.
For this the longitude of the two Vertexs
have to be found first.
For triangle PAVa:
Cos P = Tan lat A / tan lat Va
Cos P = tan 49 / tan 55
P or the d.long between A to Va
= 36°20.5E
Therefore the Longitude of the First
Vertex (Va) would be:
Longitude
of A + d.long = 30°E + 36°20.5 = 66°20.5
For triangle PAVb:
Cos P = Tan lat B / tan lat Vb
Cos P = tan 50 / tan 55
P or the d.long between B to Vb = 33°26.3
Therefore the Longitude of the First Vertex (Vb) would
be:
Longitude of B - d.long = 120°E -
33°26.3
= 86°33.7
D.long between the longitudes of Va
and Vb
D long: 86°33.7 - 66°20.5
Distance VaVb = dep = d.long
x cos lat
Distance = 688NM
So adding up all the distances: 1327 + 2298 + 688 =
4313 NM